


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)

\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)

Để hàm số ![]() có đúng 3 cực trị thì hàm số
có đúng 3 cực trị thì hàm số ![]() có 2 cực trị trái dấu.
có 2 cực trị trái dấu.
Trước hết cần điều kiện m-1≠0
⇔m≠1
Ta có ![]()
Để hàm số
![]() có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu
có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu ![]()
Kết hợp điều kiện ![]()
Khi m=1 thì hàm số trở thành ![]() có 1 cực trị Khi đó hàm số
có 1 cực trị Khi đó hàm số ![]() có đúng 3 điểm cực trị.
có đúng 3 điểm cực trị.
Vậy m∈-2;-1;0;1
Chọn C

Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
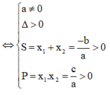
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
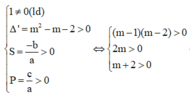
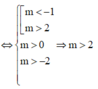
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

Đáp án C
TH1: ![]() suy ra
suy ra ![]() hàm số có
hàm số có ![]() điểm cực đại
điểm cực đại ![]() nhận m=0.
nhận m=0.
TH2: ![]() .
.
Theo yêu cầu bài toán
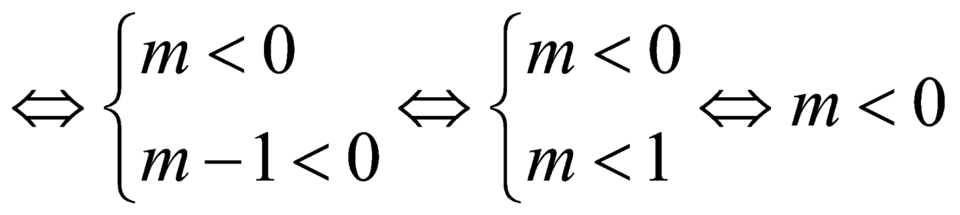 .
.
Vậy ![]() là giá trị cần tìm.
là giá trị cần tìm.