Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
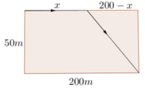
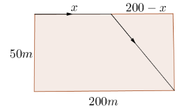
Gọi quãng đường vận động viên chạy trên bờ là x (m)
Khi đó quãng đường vận động viên đó bơi dưới nước sẽ là 50 2 + 200 − x 2 (m)
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là



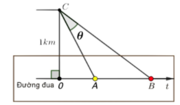
Khi tàu dừng lại thì v = 0 ⇔ 200 - 20 t = 0 ⇔ t = 10 s .
Ta có phương trình chuyển động với tại thời điểm đang xét với t 0 ∈ 0 ; 10
S = ∫ 0 t 0 v t d t = 100 t - 20 t 2 2 0 t 0 = 200 t = 10 t 0 2
Khi đó
S = 750 ⇔ 10 t 0 2 + 200 t 0 - 750 = 0 ⇒ t 0 = 5
vì t 0 ∈ 0 ; 10
Lệch nhau: 10 - 5 = 5s
Đáp án A

Đáp án A.
v t = ∫ a t d t = ∫ 6 t d t = 3 x 3 + C .
Vì v 0 = 10 ⇒ v t = 3 t 2 + 10
s t = ∫ 0 10 v t d t = ∫ 0 10 3 t 2 + 10 d t = t 3 + 10 t 10 0 = 1100 m .

Đáp án A.
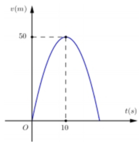
Gọi (P): y = a x 2 + b x + c là phương trình parabol
Vì (P) đi qua gốc O và đỉnh I(10;50)
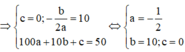
Suy ra phương trình (P) là 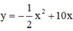
Vậy 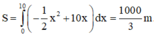

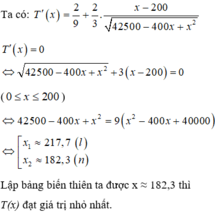

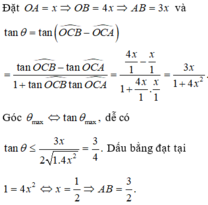


Đáp án C.
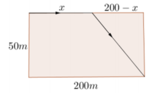
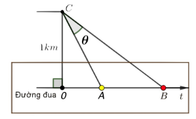
Gọi quãng đường vận động viên chạy trên bờ là x (m).
Khi đó quãng đường vận động viên bơi dưới nước sẽ là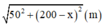
Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là
Yêu cầu bài toán tương đương với: tìm x để đạt giá trị nhỏ nhất.
Lập bảng biến thiên ta được x ≈ 182 , 3 m thì T(x) đạt giá trị nhỏ nhất.