KB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
3 tháng 4 2017
Gọi độ dài 3 cạnh của tam giác thứ tự là a,b,c (a > 0; b > 0; c > 0).
Vì độ dài 3 cạnh tỉ lệ với 3, 4, 9 nên:
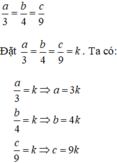
Suy ra: a + b = 3k + 4k = 7k < 9k (hay a + b < c)
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại)
Vậy không có tam giác nào có 3 cạnh tỉ lệ 3;4;9.
NM
0
NT
0
12 tháng 10 2017
Gọi độ dài 3 cạnh của tam giác thứ tự là a, b, c.
Theo đề bài ta có: a3=b4=c9a3=b4=c9
Đặt các tỉ số trên là k. Ta có:
a3=k⇒a=3ka3=k⇒a=3k
b4=k⇒b=4kb4=k⇒b=4k
c9=k⇒c=9kc9=k⇒c=9k
Suy ra: a + b = 3k + 4k = 7k < 9k
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại).
Vậy không có tam giác nào có 3 cạnh tỉ lệ với 3; 4; 9.
HT
26 tháng 2 2017
a) gọi 3 cạnh của tam giác lần lượt là a;b;c ta có
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a+b+c =60
áp dụng tích chất của dãy tỉ số bằng nhau ta có
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
\(\frac{a}{3}=5=>a=15\)
\(\frac{b}{4}=5=>b=20\)
\(\frac{c}{5}=5=>c=25\)
KH
26 tháng 2 2017
a, Gọi 3 cạnh của tam giác lần lượt là x, y, t
Ta có: \(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}\)và \(x+y+t=60\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}=\frac{x+y+t}{3+4+5}=\frac{60}{2}=5\)
\(\frac{x}{3}=5\Rightarrow a=15\)
\(\frac{y}{4}=5\Rightarrow a=20\)
\(\frac{t}{5}=5\Rightarrow a=25\)
8 tháng 3 2023
Gọi độ dài ba cạnh lần lượtlà a,b,c
Theo đề, ta co: a/2=b/3=c/4
Áp dụng tính chất của DTSBN, ta được;
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)
=>a=12; b=18; c=24
VN
8 tháng 3 2023
Gọi \(a,b,c\) lần lượt là độ dài 3 cạnh của 1 tam giác
Theo bài ra ta có :
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\) và \(a+b+c=54\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{54}{9}=6\)
\(\Rightarrow\left\{{}\begin{matrix}a=6\times2=12\\b=6\times3=18\\c=6\times4=24\end{matrix}\right.\)
Vậy \(12,18,24\) lần lượt là độ dài 3 cạnh của 1 tam giác .
28 tháng 11 2015
1) Goi x,y,z lan luot la cac goc cua tam giac tren. ta lap duoc:
x/3=y/5=z/7
Gia xu 60 do la so do cua goc thu nhat thi ta suy ra: x/3=y/5=z/7=60/3=20
=> x=60 ; y=100 ; z=140
Do 60+100+140 khong bang 180 nen tam giac nay khong ton tai.
Gia xu 60 do la so do cua goc thu 2 thi suy ra: x/3=y/5=z/7=60/5=12
=> x=36 ; y=60 ; z=84
Do 36+60+84 bang 180 nen tam giac nay ton tai
Gia xu 60 la so do cua goc thu 3 thi suy ra: x/3=y/5=z/7=60/7
=> x=180/7 ; y=300/7 ; z=60
Do 180/7+300/7+60 khong bang 180 nen tam giac nay khong ton tai
Vay tam giac tren chi co the ton tai khi goc thu 2 hay goc ti le voi 5 cua no co so do la 60 do.
2) goi cac canh cua tam giac nay lan luot la a,b,c. Theo de bai ta co:
a=3k ; b=4k ; c=8k
Vi a+b ( hay 3k+4k=7k) < c ( hay 8k ) nen tam giac nay khong ton tai
S
17 tháng 1 2018
Theo bài ra ta có: \(\frac{AB}{9}=\frac{AC}{12}=\frac{BC}{15}\)
Đặt \(\frac{AB}{9}=\frac{AC}{12}=\frac{BC}{15}=k\Rightarrow AB=9k;AC=12k;BC=15k\)
Ta có: \(AB^2+AC^2=\left(9k\right)^2+\left(12k\right)^2=9^2k^2+12^2k^2=k^2\left(9^2+12^2\right)=225k^2\left(1\right)\)
\(BC^2=\left(15k\right)^2=225k^2\left(2\right)\)
Từ (1) và (2) => \(AB^2+AC^2=BC^2\)
=> tam giác ABC vuông tại A (theo định lý pytago đảo)
18 tháng 2 2019
AB;AC;BC tỉ lệ với 9;12;15(gt)
=>AB/9=AC/12=BC/15
=>AB^2/9^2=AC^2/12^2=BC^2/15^2
=>AB^2/81=AC^2/144=BC^2/225
=>AB^2+AC^2/81+144=BC^2/225
=>AB^2+AC^2/225=BC^2/225
=>AB^2+AC^2=BC^2
=> Tam giác ABC là tam giác vuông tạiA
8 tháng 1 2018
có hay không một tam gaics mà ba cạnh của nó:
a) tỉ lệ thuận với các số 3; 4; 8?
b) Tỉ lệ thuận với các số 1/3; 1/4; 1/8?
Trả lời:
a) Đéo
b) Đéo
Giả sử là có thì gọi 3 cạnh là a;b;c
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{9}=k\)
a+b>c
3k+4k>9k
7k>9k
Vô lí vậy thật là ... à nhầm ko có