Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Gọi vận tốc của vận động viên chạy và vận động viên đua xe đạp là: v1, v2 (v1> v2> 0). Khoảng cách giữa hai vận động viên chạy và hai vận động viên đua xe đạp là l1, l2 (l2>l1>0). Vì vận động viên chạy và vận động viên đua xe đạp chuyển động cùng chiều nên vận tốc của vận động viê đua xe khi chộn vận động viên chạy làm mốc là:
v21= v2 - v1 = 10 - 6 = 4 (m/s).
- Thời gian hai vận động viên đua xe vượt qua một vận động viên chạy là:
\(t_1=\frac{l_2}{v_{21}}=\frac{20}{4}=5\)(s)
- Thời gian một vận động viên đua xe đạp đang ở ngang hàng một vận động viên chạy đuổi kịp một vận động viên chạy tiếp theo là:
\(t_1=\frac{l_2}{v_{21}}=\frac{10}{4}=2,5\) (s)

a,Thời gian để chạy là:
\(t=\dfrac{s}{t}=\dfrac{100}{10}=10\left(s\right)\)
b,Thời gian để chạy là:
\(t=\dfrac{s}{t}=\dfrac{60}{10}=6\left(s\right)\)

Vì xe tải chở hàng hóa có trọng lượng lớn nên có quán tính lớn. Vì thế xe sẽ tăng tốc rất chậm. Còn vận động viên có trọng lượng nhỏ hơn rất nhiều nên tăng tốc sẽ rất nhanh.
Mà chặng đường là 10 m (rất ngắn) nên có thể chắc chắn rằng vận động viên sẽ chiến thắng
Theo mình thì chiếc xe tải chở đầy hàng hóa thắng cuộc vì :
Mặc dù chở đầy hàng hóa nhưng vận tốc xe tải giảm không đáng kể.
Còn vận động viên thì có vận tốc nhỏ hơn xe tải

Vận tốc trung bình của vận động viên trong mỗi khoảng thời gian là:
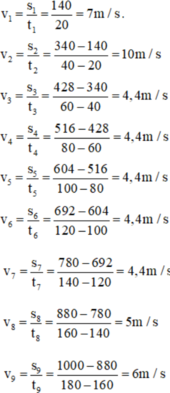
Dựa vào kết quả trên, ta thấy:
Trong hai quãng đường đầu: vận động viên chuyển động nhanh dần.
Trong năm quãng đường sau: vận động viên chuyển động đều.
Hai quãng đường sau cùng: vận động viên chuyển động nhanh dần.

Mình xin lỗi bạn nhé , bạn sửa lại giúp mình : vậy vận động viên A chạy nhanh hơn
đổi \(12m/s=43,2km/h\)\(\)(vận tốc VĐV A )
ta thấy \(Va>Vb\left(43,2>36\right)\)
nên VĐV A chạy nhanh hơn

a) Thời gian người thứ nhất chạy đến đích là:
\(t_1=\dfrac{\dfrac{1}{2}s}{12}+\dfrac{\dfrac{1}{2}s}{8}=\dfrac{5}{48}s\left(h\right)\)
Thời gian người thứ hai chạy hết quãng đường đầu là:
\(\dfrac{1}{2}t_2=\dfrac{s_1}{8}\left(h\right)\)
Thời gian người thứ hai chạy hết quãng đường sau là:
\(\dfrac{1}{2}t_2=\dfrac{s_2}{12}\left(h\right)\)
Từ đây ta có: \(\dfrac{1}{2}t_2=\dfrac{s_1}{8}=\dfrac{s_2}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\Rightarrow\dfrac{1}{2}t_2=\dfrac{s_1}{8}=\dfrac{s_2}{12}=\dfrac{s_1+s_2}{8+12}=\dfrac{s}{20}\Rightarrow t_2=\dfrac{1}{10}s\left(h\right)\)
So sánh: \(\dfrac{1}{10}s< \dfrac{5}{48}s\Rightarrow t_1< t_2\)
Vậy người thứ nhất về đích trước.
b) Đổi 2s=\(\dfrac{1}{1800}h\).
Vì người chạy chậm tới đích sau người kia 2s nên ta có:
\(\dfrac{5}{48}s-\dfrac{1}{10}s=\dfrac{1}{1800}\)
Giải phương trình trên ta được: \(s=\dfrac{2}{15}\left(km\right)\)
Vậy độ dài quãng đường là \(\dfrac{2}{15}\) km.
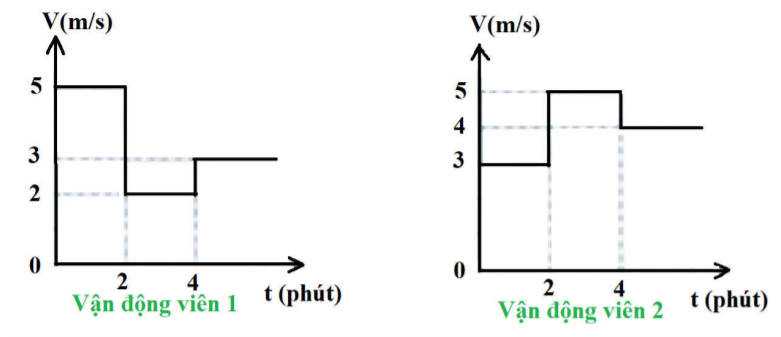


\(\left\{{}\begin{matrix}v'=s':t'=12,5:\dfrac{30}{60}=25\left(\dfrac{km}{h}\right)\\v''=s'':t''=15:\dfrac{45}{60}=20\left(\dfrac{km}{h}\right)\end{matrix}\right.\)
Ta thấy: \(v'>v''\left(25>20\right)=>\) VĐV1 chạy nhanh hơn.