

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án: A
Ta có:
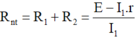
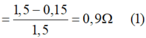
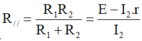
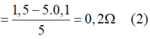
Từ (1) và (2) ⇒ R 1 R 2 = 1 , 8 Ω (3)
Từ (1) và (3)
⇒ R 1 = 0 , 3 Ω ; R 2 = 0 , 6 Ω h o ặ c R 1 = 0 , 6 Ω ; R 2 = 0 , 3 Ω

Lúc đầu chỉ có một nguồn nên: I = E R + r → R = r I = 2 A 2 = E 2 r ⇒ E r = 4 ( 1 )
Khi mắc 3 nguồn song song thì
E b = E r b = r b ⇒ I = E b R + r b = E R + r b = 3 E 4 r → ( 1 ) I = 3 4 .4 = 3 ( A )
Chọn A

Theo sơ đồ Hình 10.6a và nếu R = r thì dòng điện chạy qua R có cường độ là:
![]()
Theo sơ đồ Hình 10.6b và nếu R = r thì dòng điện chạy qua R có cường độ là:
![]()
Từ (1) và (2) cho ta điều phải chứng minh

Mắc hai nguồn nối tiếp:
\(\xi_b=n\cdot\xi=2\xi\)
\(r_b=n\cdot r=2r\)
\(\Rightarrow I_1=\dfrac{\xi_{b1}}{r_{b1}}=\dfrac{2\xi}{2r}=\dfrac{\xi}{r}\)
Mắc song song:
\(\xi_b=\xi\)
\(r_b=\dfrac{r}{n}=\dfrac{r}{2}\)
\(\Rightarrow I_2=\dfrac{\xi_{b2}}{r_{b2}}=\dfrac{\xi}{\dfrac{r}{2}}=2\cdot\dfrac{\xi}{r}=2I_1\)
\(\Rightarrow\dfrac{I_1}{I_2}=\dfrac{1}{2}\)
Mắc hai nguồn nối tiếp:
\(\xi_b=n\cdot\xi=2\xi\)
\(r_b=n\cdot r=2r\)
\(\Rightarrow I_1=\dfrac{\xi_b}{r_{b1}+r}=\dfrac{2\xi}{3r}\)
Mắc hai nguồn song song:
\(\xi_b=\xi\)
\(r_b=\dfrac{r}{n}=\dfrac{r}{2}\)
\(\Rightarrow I_2=\dfrac{\xi_{b2}}{r_{b2}+r}=\dfrac{\xi}{\dfrac{r}{2}+r}=\dfrac{\xi}{\dfrac{3}{2}r}=\dfrac{2}{3}\cdot\dfrac{\xi}{r}\)
Vậy \(\dfrac{I_1}{I_2}=1\)
Chọn C