Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần lập là A = a 1 a 2 a 3 a 4 a 5 với 1 ≤ a 1 ≤ 2 .
+ Trường hợp 1: a 1 = 1.
Có 4 cách chọn a 5 và A 5 3 cách chọn các chữ số còn lại nên có 4 . A 5 3 số.
+ Trường hợp 2: a 1 = 2; a 2 lẻ.
Có 2 cách chọn a 2 , 3 cách chọn a 5 và A 4 2 cách chọn các chữ số còn lại nên có 2 . 3 . A 4 2 = 72 số.
+ Trường hợp 3: a 1 = 2; a 2 chẵn.
Có 2 cách chọn a 2 , 2 cách chọn a 3 và A 4 2 cách chọn các chữ số còn lại nên có 2 . 2 . A 4 2 = 48 số.
Vậy có 240 + 72 + 48 = 360 số
Đáp án A

Đáp án C
Gọi số tự nhiên cần lập có dạng a b c ¯ a , b , c ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; a ≠ 0
Bài toán không yêu cầu số tự nhiên có 3 chữ số khác nhau.
Chọn c = {0;2;4;6} có 4 cách chọn, chọn a ≠ 0 có 6 cách chọn và chọn b có 7 cách chọn.
Theo quy tắc nhân có: 4.6.7 = 168 số.

Đáp án A.
Gọi n = a 1 a 2 a 3 a 4 a 5 a 6 ¯ là số tự nhiên gồm 6 chữ số đôi một khác nhau được lập thành từ các chữ số 1, 2, 3, 4, 5, 6 thỏa mãn n < 432000 .
n < 432000 ⇒ a 1 có thể nhận một trong các giá trị 1, 2, 3, 4.
* a 1 ∈ 1,2,3 ⇒ a 2 , a 3 , a 4 , a 5 , a 6 là một hoán vị của 5 chữ số thuộc tập 1,2,3,4,5,6 \ a 1 . Trường hợp này có 3.5! = 360 số.
* a 1 = 4 ⇒ a 2 có thể nhận một trong các giá trị 1, 2, 3.
+ a 2 ∈ 1,2 ⇒ a 3 , a 4 , a 5 , a 6 là một hoán vị của 4 chữ số thuộc tập 1,2,3,4,5,6 \ a 1 , a 2 . Trường hợp này có 2.4 ! = 48 số.
+ a 2 = 3 ⇒ a 3 chỉ có thể nhận giá trị bằng 1. Khi đó a 4 , a 5 , a 6 là một hoán vị của 3 chữ số thuộc tập 2,5,6 . Trường hợp này có 3 ! = 6 số.
Vậy theo quy tắc cộng có tất cả 360 + 48 + 6 = 414 số.





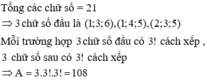


Đáp án A
Ta có các TH sau
TH1: Số tự nhiên có 1 chữ số, có 5 chữ số.
TH2: Số tự nhiên có 2 chữ số, có 4.5 = 20 số.
TH3: Số tự nhiên có 3 chữ số, có 4.5 2 = 100 số.
Suy ra có tất cả 5 + 20 + 100 = 125 số thỏa mãn đề bài