Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
![]()
Suy ra ABCD là hình bình hành.
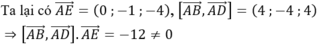
=>E.ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.

Tính \(I=\int_0^{\dfrac{\pi}{2}}\dfrac{cos^{2017}x}{sin^{2017}x+cos^{2017}}dx\left(1\right)\)
Đặt \(t=cosx\Rightarrow sinx=\sqrt{1-cos^2x}\)
\(\Rightarrow dt=-sinx.dx\)
\(\Rightarrow I=\int_0^1\dfrac{t^{2017}.}{\sqrt{1-t^2}.\left(\left(\sqrt{1-t^2}\right)^{2017}+t^{2017}\right)}dt\)
Đặt: \(t=siny\Rightarrow\sqrt{1-t^2}=cosy\)
\(\Rightarrow dt=cosy.dy\)
\(\Rightarrow I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}y.cosy}{cosy\left(cos^{2017}y+sin^{2017}y\right)}dy=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}y}{\left(cos^{2017}y+sin^{2017}y\right)}\)
\(\Rightarrow I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}x}{\left(cos^{2017}x+sin^{2017}x\right)}\left(2\right)\)
Cộng (1) và (2) ta được
\(2I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}x+cos^{2017}x}{sin^{2017}x+cos^{2017}x}dx=\int_0^{\dfrac{\pi}{2}}1dx\)
\(=x|^{\dfrac{\pi}{2}}_0=\dfrac{\pi}{2}\)
\(\Rightarrow I=\dfrac{\pi}{4}\)
Thế lại bài toán ta được
\(\dfrac{\pi}{4}+t^2-6t+9-\dfrac{\pi}{4}=0\)
\(\Leftrightarrow t^2-6t+9=0\)
\(\Leftrightarrow t=3\)
Chọn đáp án C
mỗi trắc nghiệm thoy mà lm dài ntn s @@
chắc lên đó khó lắm ag

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

4.
\(xy+y=2\Leftrightarrow xy=2-y\Rightarrow x=\frac{2-y}{y}=\frac{2}{y}-1\)
\(\Rightarrow P=x+y^2=y^2+\frac{2}{y}-1\)
\(\Rightarrow P=y^2+\frac{1}{y}+\frac{1}{y}-1\ge3\sqrt[3]{\frac{y^2}{y.y}}-1=2\)
\(\Rightarrow P_{min}=2\) khi \(x=y=1\)
Chọn đáp án A.