Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x^2y-8x+y-4\right)log_3y=2log_3\dfrac{\sqrt{8x-y+4}}{x}-log_3y=log_3\dfrac{8x-y+4}{x^2y}\)
\(\Rightarrow log_3\left(x^2y\right)+x^2y.log_3y=log_3\left(8x-y+4\right)+\left(8x-y+4\right)log_3y\)
Xét hàm \(f\left(t\right)=log_3t+t.log_3y\Rightarrow f'\left(t\right)=\dfrac{1}{1.ln3}+log_3y>0\)
\(\Rightarrow x^2y=8x-y+4\)
\(\Rightarrow y=\dfrac{8x+4}{x^2+1}\)
Tìm y để pt trên có nghiệm lớn hơn 1, lập BBT \(\Rightarrow y< 6\)

ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\3^x-9\ge0\end{matrix}\right.\) \(\Rightarrow x\ge2\)
BPT tương đương:
\(\left[{}\begin{matrix}3^x-9=0\\log_3x-y\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\log_3x\le y\end{matrix}\right.\)
Do \(x\ge2\) mà ko có quá \(2186\) số nguyên x thỏa mãn \(\Rightarrow x\le2187\)
\(\Rightarrow3^y\le2187\Rightarrow y\le7\)
Có 7 số nguyên dương y thỏa mãn
Có bao nhiêu số nguyên y sao cho tồn tại x∈ (\(\dfrac{1}{2}\) ;8) thỏa mãn 92\(x^2\)+xy= (1+xy).915x

\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)
Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)
Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)
Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)
Do đó:
\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)
\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)
\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)
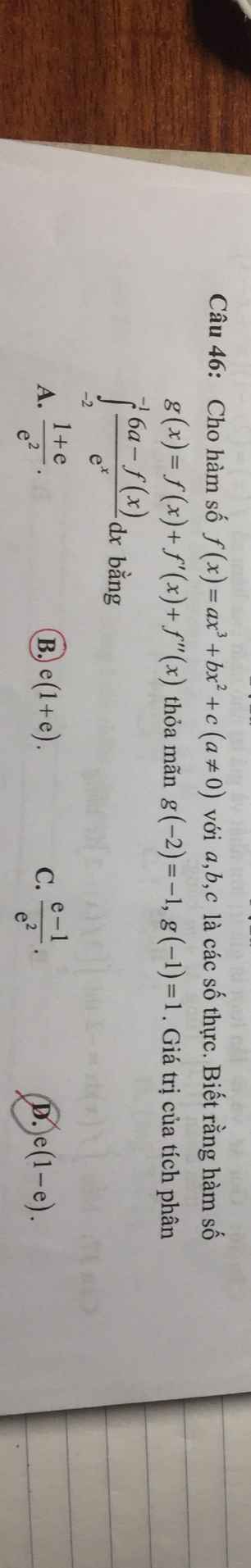
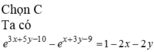

Đặt \(log_3\left(x+y\right)=log_2\left(x^3+y^3\right)=a\Rightarrow\left\{{}\begin{matrix}x+y=3^a\\x^3+y^3=2^a\end{matrix}\right.\)
\(2^a=\left(x+y\right)^3-3xy\left(x+y\right)=3^{3a}-3^{a+1}xy\)
\(\Rightarrow xy=\frac{3^{3a}-2^a}{3^{a+1}}\)
Mặt khác \(\left(x+y\right)^2\ge4xy\Rightarrow3^{2a}\ge\frac{4\left(3^{3a}-2^a\right)}{3^{a+1}}\)
\(\Leftrightarrow3^{3a+1}\ge4.3^{3a}-2^{a+2}\)
\(\Leftrightarrow2^{a+2}\ge3^{3a}\)
\(\Leftrightarrow\left(a+2\right)ln2\ge3a.ln3\)
\(\Rightarrow a\le\frac{2ln2}{3ln3-ln2}\)
\(\Rightarrow x+y=3^a< 2\) \(\Rightarrow x=1\)
Có duy nhất 1 số nguyên dương x