Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=3x^2+m+\dfrac{1}{x^6}\ge0\) ; \(\forall x>0\)
\(\Leftrightarrow3x^2+\dfrac{1}{x^6}\ge-m\)
\(\Leftrightarrow-m\le\min\limits_{x>0}\left(3x^2+\dfrac{1}{x^6}\right)\)
Ta có: \(3x^2+\dfrac{1}{x^6}=x^2+x^2+x^2+\dfrac{1}{x^6}\ge4\sqrt[4]{\dfrac{x^6}{x^6}}=4\)
\(\Rightarrow-m\le4\Rightarrow m\ge-4\)

Tập xác định D=R\{m}.
Ta có 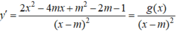
Hàm số đồng biến trên 1 ; + ∞ khi và chỉ khi g x ≥ 0 v à m ≤ 1 (1)
Vì ∆ ' g = 2 ( m + 1 ) 2 ≥ 0 , ∀ m nên (1) tương đương g(x)=0 có hai nghiệm thỏa x 1 ≤ x 2 ≤ 1
Điều kiện tương đương là
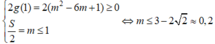
Do đó không có giá trị nguyên dương của m thỏa yêu cầu bài toán.
Chọn D.

Đáp án: C.
Tập xác định: D = R. y' = 3 x 2 - 6x + m.
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R
⇔ 3 x 2 - 6x + m = 0 có hai nghiệm phân biệt
⇔ ∆ ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3

Đáp án: C.
Tập xác định: D = R. y' = 3 x 2 - 6x + m.
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên R
⇔ 3 x 2 - 6x + m = 0 có hai nghiệm phân biệt
⇔ Δ' = 9 - 3m > 0 ⇔ 3m < 9 ⇔ m < 3



Xét trên miền \(\left(1;+\infty\right)\):
ĐKXĐ: \(x^3-mx+1>0\)
\(\Leftrightarrow x^3+1>mx\Leftrightarrow x^2+\frac{1}{x}>m\) \(\forall x\in\left(1;+\infty\right)\)
\(\Leftrightarrow m< \min\limits_{\left(1;+\infty\right)}f\left(x\right)\)
\(f\left(x\right)=x^2+\frac{1}{x}\Rightarrow f'\left(x\right)=2x-\frac{1}{x^2}=0\Rightarrow x=\frac{1}{\sqrt[3]{2}}\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(\left(1;+\infty\right)\)
\(\Rightarrow f\left(x\right)>f\left(1\right)=2\Rightarrow m\le2\)
Có 2 giá trị nguyên dương của m là \(m=\left\{1;2\right\}\) thỏa mãn
Sao lại có m=2 nữa ạ, em tưởng m<2 thôi