Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
cho em hỏi là tại sao m≠0 mà đkxđ của m lại là -3<m<3 ạ ?

Tìm tất cả các giá trị nguyên của m để hàm số y=x^8+(m-2)x^5-(m^2-4)x^4+1 đạt cực tiểu tại x=0.
m= 2
nha bạn
bạn muốn tl rõ hơn thì bạn tìm trên google

Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.






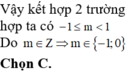
Đáp án B
Dễ thấy x=0 là một nghiệm của đạo hàm y'. Do đó hàm số đạt cực tiểu tại x=0 khi và chỉ khi y'đổi dấu từ âm sang dương khi đi qua nghiệm x=0.Ta thấy dấu của y' là dấu của hàm số g ( x ) = x 2 - 4 2 m - 1 x - m . Hàm số g(x) đổi dấu khi đi qua giá trị x=0 khi x=0 là nghiệm của g(x). Khi đó g(0) = 0 ⇔ m=0
Thử lại, với m=0 thì g ( x ) = x 2 + 4 x đổi dấu từ âm sang dương khi đi qua giá trị x=0
Vậy có 1 giá trị m thỏa mãn yêu cầu bài toán