K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
3 tháng 8 2019
Chọn B.
Phương pháp:

Bảng biến thiên:
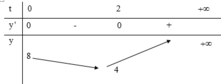
Phương trình đã cho có 3 nghiệm ⇔ phương trình ẩn t có hai nghiệm phân biệt trong đó có một nghiệm bằng 0 và một nghiệm dương ⇔ đường thẳng y = 2-m cắt đồ thị hàm số tại một điểm có hoành độ bằng 0 và điểm còn lại có hoành độ dương.

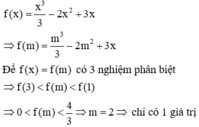


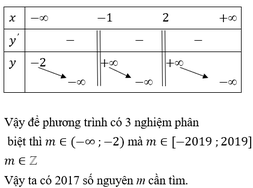



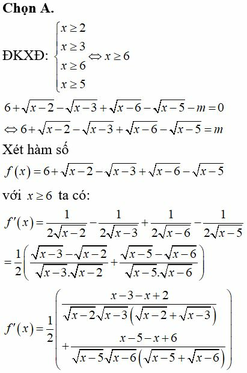

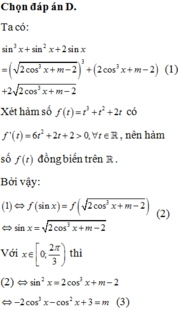

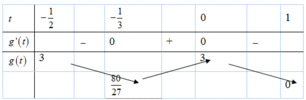



Ta có
9 . 3 2 x - m ( 4 x 2 + 2 x + 1 4 + 3 m + 3 ) . 3 x + 1 = 0 ⇔ 3 x + 1 + 1 3 x + 1 - m 3 4 x + 1 + 3 m + 3 = 0 1
Đặt t=x+1, phương trình (1) thành
3 t + 1 3 t - m 3 4 x + 1 + 3 m + 3 = 0 2
Bài toán trở thành tìm số giá trị nguyên của m để phương trình (2) có đúng 3 nghiệm thực phân biệt.
Nhận xét: Nếu t 0 là một nghiệm của phương trình (2) thì - t 0 cũng là một nghiệm của phương trình (2). Do đó điều kiện cần để phương trình (2) có đúng 3 nghiệm thực phân biệt là phương trình (2) có nghiệm t=0.
Với t=0 thay vào phương trình (2) ta có
- m 2 - m + 2 = 0 ⇔ [ m = 1 m = - 2
Thử lại:
+) Với m=-2 phương trình (2) thành 3 t + 1 3 t + 2 3 4 t - 3 = 0
Ta có 3 t + 1 3 t ≥ 2 , ∀ t ∈ ℝ và 2 3 4 t - 3 = 0 , ∀ t ∈ ℝ suy ra 3 t + 1 3 t + 2 3 4 t - 3 = 0 ≥ 0 , ∀ t ∈ ℝ
Dấu bằng xảy ra khi t=0, hay phương trình (2) có nghiệm duy nhất t=0 nên loại m=-2
+) Với m=1 phương trình (2) thành 3 t + 1 3 t + 1 3 4 t + 6 = 0 ( 3 )
Dễ thấy phương trình (3) có 3 nghiệm t=-1,t=0,t=1
Ta chứng minh phương trình (3) chỉ có 3 nghiệm t=-1,t=0,t=1.Vì t là nghiệm thì -t cũng là nghiệm phương trình (3) nên ta chỉ xét phương trình (3) trên [ 0 ; + ∞ )
Trên tập [ 0 ; + ∞ ) ,(3) ⇔ 3 t + 1 3 t + 1 3 4 t + 6 = 0
Xét hàm f ' ( x ) = 3 t + 1 3 t + 1 3 4 t + 6 trên [ 0 ; + ∞ )
Ta có
f ' ( t ) = 3 t ln 3 - 3 - t . ln 3 - 2 3 t , f ' ' ( t ) = 3 t ln 2 3 + 3 - t . ln 2 3 + 1 3 . t 3 > 0 , ∀ t > 0
Suy ra f '(t) đồng biến trên ( 0 ; + ∞ ) ⇒ f ' ( t ) = 0 có tối đa 1 nghiệm t > 0 ⇒ f ( t ) = 0 có tối đa 2 nghiệm t ∈ [ 0 ; + ∞ ) . Suy ra trên [ 0 ; + ∞ ) , phương trình (3) có 2 nghiệm t=0, t=1
Do đó trên tập ℝ , phương trình (3) có đúng 3 nghiệm t=-1,t=0,t=1. Vậy chọn m=1
Chú ý: Đối với bài toán trắc nghiệm này, sau khi loại được m=-2 ta có thể kết luận đáp án C do đề không có phương án nào là không tồn tại m.
Chọn đáp án C.