

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
Ta có:

Tập hợp điểm M biểu diễn w là trung trực của ![]() nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
![]()
Đặt ![]()
Do ω ⩾ 2 5 nên M nằm ngoài đường tròn tâm O bán kính R= 2 5
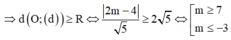

Đáp án D
Phương pháp giải:
Đặt z=a+bi thực hiện yêu cầu bài toán, chú ý số phức là số thực khi phần ảo bằng 0
Lời giải:
Ta có ![]()
Khi đó
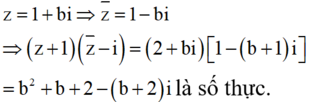
Khi và chỉ khi b + 2 = 0 ⇔ b = - 2
Vậy S=a+2b= -3

Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)
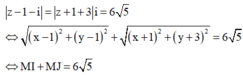
![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
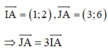
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
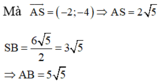
Vậy ![]()

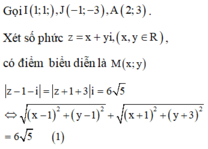
↔ M I + M J = 6 5 nên M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là 3 5
Tìm giá trị lớn nhất của z - 2 - 3 i tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip
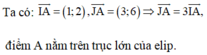
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.

Đáp án D

Đáp án D
Phương pháp.Sử dụng giả thiết để tìm được ![]()
Thay vào ![]() và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
m
0
và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
m
0
Lời giải chi tiết.
Giả sử ![]() . Khi đó ta có
. Khi đó ta có
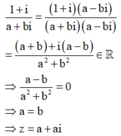
Thay vào ![]() Ta nhận được
Ta nhận được
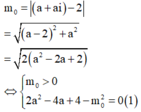
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a.
Khi đó phương trình (1) phải thỏa mãn

Kết hợp với điều kiện ![]() ta suy ra giá trị cần tìm là
ta suy ra giá trị cần tìm là ![]()
Sai lầm.Một bộ phận nhỏ học sinh vẫn có thể quên đưa ra điều kiện ![]() nên hai nghiệm là
nên hai nghiệm là ![]()