Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gỉa sử cả 22 quyển đều là sách Toán thì số trang sẽ là :
150 x 22 = 3300 ( trang )
Số trang dôi ra là :
3300 - 3120 = 180 ( trang )
Thay một quyển sách Văn bằng một quyển sách Toán thì số trang tăng là :
150 - 132 = 18 ( trang )
Số sách Văn là :
180 : 18 = 10 ( quyển )
Số sách Toán là :
22 - 10 = 12 ( quyển )
Đáp số : Văn : 10 quyển sách.
: Toán : 12 quyển sách.
gọi số sách văn là x
=> số sách toán là:22-x
ta có phương trình :
x .132 +(22 - x).150 = 3120
132x + 3300 - 150x=3120
-18x = -180
x = 10
vậy có 10 sách văn,12 sách toán
tích mình nha :v
ak dấu . là dấu nhân nhé![]()

HD: Xếp 10 quyển sách tham khảo thành một hàng ngang trên giá sách có : 10! cách sắp xếp.
Sắp xếp 2 cuốn toán 1 và toán 2 cạnh nhau có 2! cách,
Sắp xếp 6 cuốn sách Toán sao cho có hai quyển Toán T1 và Toàn T2 cạnh nhau có 2!.5! cách.
Khi đó có 4 vị trí để sắp xếp 3 cuốn Anh ở giữa hai quyển Toán và 3 cách sắp xếp cuốn Tiếng Anh.
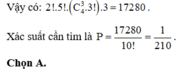

Đáp án A
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5 ! .2 ! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240. A 4 3 .3 10 ! = 1 210 .

Chọn B.
TH1: 3 quyển được chọn có 2 quyển sách Văn, 1 quyển sách Toán.
Chọn 2 quyển Văn trong 6 quyển Văn khác nhau có 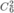 cách.
cách.
Chọn 1 quyển Toán trong 10 quyển Toán khác nhau có 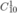 cách.
cách.
Áp dụng quy tắc nhân, có 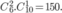
TH2: 3 quyển được chọn có 2 quyển sách Toán, 1 quyển sách Văn.
Chọn 1 quyển Văn trong 6 quyển Văn khác nhau có 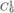 cách.
cách.
Chọn 2 quyển Toán trong 10 quyển Toán khác nhau có 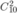 cách.
cách.
Áp dụng quy tắc nhân, có 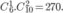
Vậy số cách chọn ra 3 quyển sách trong đó có đúng 2 quyển cùng loại là 150 + 270 = 420.


Số sách trong 5 thùng sách là
5x306=1530 (quyển sách)
Số quyển sách mỗi thư viện được chia là:
1530:9=170 (quyển sách)
Đáp số: 170 quyển sách