Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chữ " b" mk ghi ở phần b) trước "CMR " là gõ nhầm đấy, ko liên quan j đến bài toán đâu !!

\(\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)\ge2\sqrt{2a^2}\cdot2\sqrt{2b^2}\cdot2\sqrt{2c^2}=8abc\sqrt{8}=16abc\sqrt{2}\left(đpcm\right)\)
Dấu \("="\Leftrightarrow a=b=c=\sqrt{2}\)

Xét phương án C:
(C) tiếp xúc với trục Oy khi d ( I ; y ' O y ) = R ⇔ a = R .
Do đó đáp án (C) sai vì nếu a= -9 => R= -9 < 0 (vô lý)
Chọn C.

Giả sử không có BĐT thức nào có nghiệm. Khi đó:
\(\Delta_1=\left(2b\right)^2-4ac=4b^2-4ac< 0\Leftrightarrow b^2< ac\left(1\right)\)
\(\Delta_2=\left(2c\right)^2-4ab=4c^2-4ab< 0\Leftrightarrow c^2< ab\left(2\right)\)
\(\Delta_3=\left(2a\right)^2-4bc=4a^2-4bc< 0\Leftrightarrow a^2< bc\left(3\right)\)
Từ (1), (2), (3) suy ra b2 . c2 . a2 < ac . ab . bc (Vì các vế của chúng đều phải dương)
\(\Leftrightarrow\left(abc\right)^2< \left(abc\right)^2\), vô lí
Do đó giả thiết sai. Vậy ít nhất một trong 3 BĐT có nghiệm

Tham khảo ở đây nhé!
Trong mặt phẳng tọa độ Oxy cho điểm M(3;1). Giả sử A(a;0) và B(0;b) ( với a, b là các số thực không âm) là 2 điểm sao cho tam giác MAB vuông tại M và có diện tích nhỏ nhất. Tìm a và b
tóm lại đề bài bạn cần làm như sau
bạn tính vecto MA rồi tính vecto MB từ đó tính độ dài MA và MB
=>diện tích tam giác vuông MAB=1/2 MA.MB rồi lập luận thế thôi hết bài
lập luận không khó đâu good luck

Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.

a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
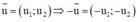
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
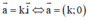
c) Đúng.