NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
26 tháng 1 2022
\(A=4+4^2+4^3+...+4^{81}=4\left(1+4+4^2\right)+...+4^{79}\left(1+4+4^2\right)\)
\(=21\left(4+...+4^{79}\right)⋮21\)vậy ta có đpcm
BT
3
26 tháng 12 2017
Các số có tận cùng 0 , 1 , 5 , 6 nâng lên lũy thừa nào ( khác 0 ) cũng có tận cùng bằng 0 , 1 , 5 , 6
6100 - 1 = .....6 - 1 = ......5 \(⋮\)5
Vậy 6100 - 1 chia hết cho 5
26 tháng 12 2017
a) Ta có:
6^100- 1=...6-1=...5 chia hết cho 5
Mà 6^100 - 1 có tận cùng là 5 nên 6^100 -1 chia hết cho 5.
b)Ta thấy 21^20 - 11^10 = .....1 - ......1 = .......0
Mà 21^20 - 11^10 có tận cùng là chữ số 0 nên 21^20-11^10 chia hết cho 2 và 5
N
4
11 tháng 11 2021
\(A=\left(1+4+4^2\right)+...+4^{57}\left(1+4+4^2\right)\)
\(=21\left(1+...+4^{57}\right)⋮7\)
11 tháng 11 2021
cứ tổng của 3 số liên tiếp được 1 số chia hết cho 7
=> (1+4+4^2)+(4^3+4^4+4^5)+.....+(4^57+4^58+4^59)(20 cặp số)
=> 21+ 4^3(1+4+4^2)+...+4^57(1+4+4^2)
......
Vì 21 chia hết cho 7=> 21.(........) chia hết cho 7=> A chia hết cho 7
đpcm
11 tháng 11 2021
\(b,A=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...\left(4^{57}+4^{58}+4^{59}\right)\\ A=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...+4^{57}\left(1+4+4^2\right)\\ A=\left(1+4+4^2\right)\left(1+4^3+...+4^{57}\right)\\ A=21\left(1+4^3+...+4^{57}\right)⋮7\)
11 tháng 11 2021
a: \(\Leftrightarrow2x+1\in\left\{1;3\right\}\)
hay \(x\in\left\{0;1\right\}\)
PT
1
CM
21 tháng 11 2019
D = 1 + 4 + 4 2 + 4 3 + . . . + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 + 4 4 + 4 5 + ... + 4 57 + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 . 1 + 4 + 4 2 + ... + 4 57 . 1 + 4 + 4 2
= 21 + 21 . 4 3 + . . . + 21 . 4 57 ⋮ 21
PT
1
NT
0
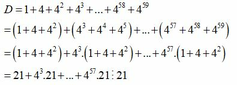
a/ A=20+21+22+.....+299+2100
=>2A=20.2+21.2+22.2+.....+299.2+2100.2=21+22+.....+2100+2101
=>2A-A=(21+22+.....+2100+2101)-(20+21+22+.....+299+2100)
=>A=2^101-1<B
b/C=2+22+23+......+2300
=>2C=21.2+22.2+.....+2299.2+2300.2=22+23+.....+2300+2301
=>2C-C=(22+23+.....+2300+2301)-(2+22+23+......+2300)
=>C=2^301-1<B