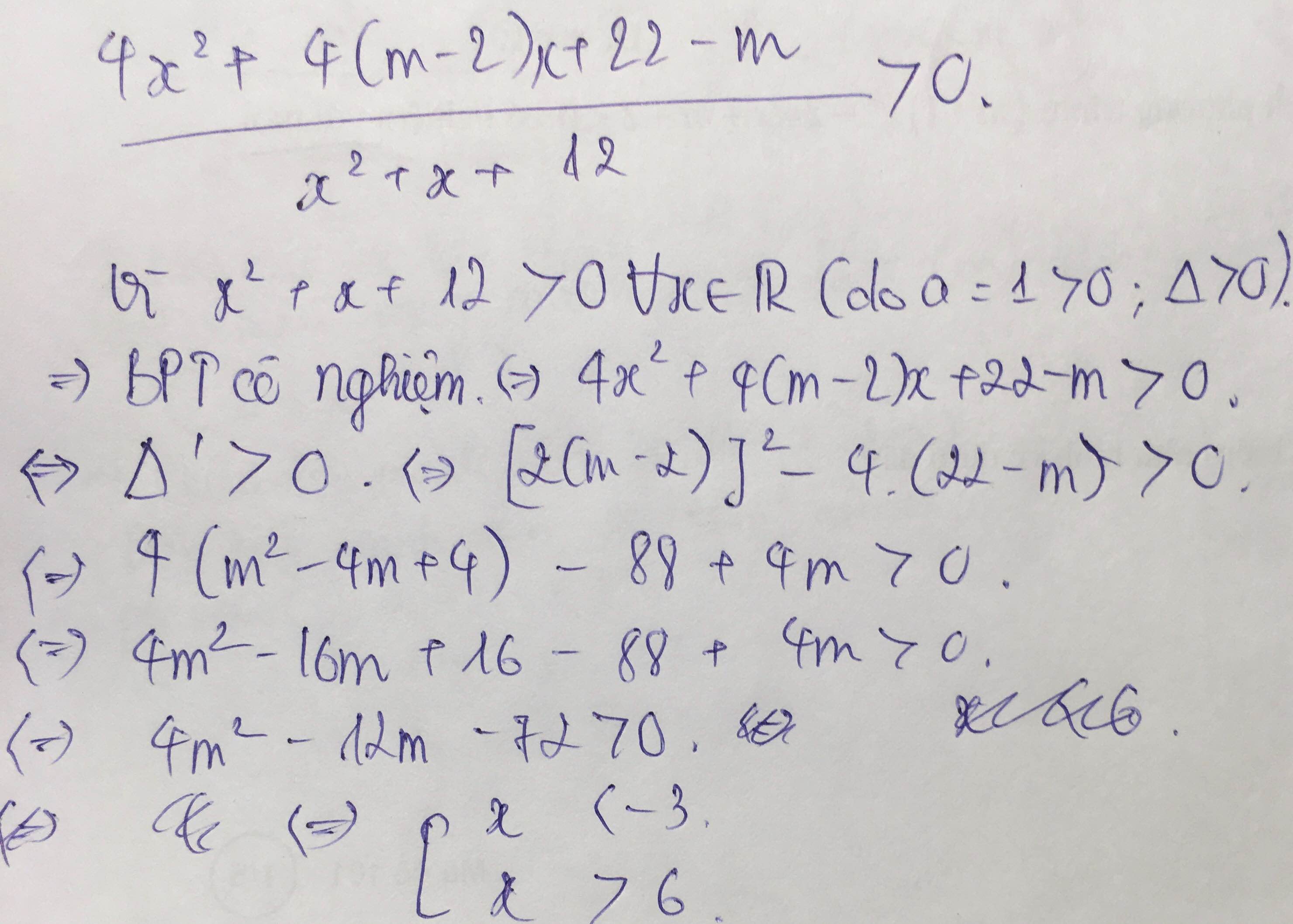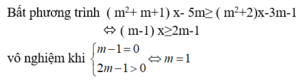Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu m >0 thì – m <0
Ta có: n <0 và – m <0 nên n + (-m) < 0 hay n – m < 0
Chọn B.

a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4

1.
Nếu \(m=0\), \(f\left(x\right)=2x\)
\(\Rightarrow m=0\) không thỏa mãn
Nếu \(x\ne0\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-1\right)^2-4m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -\dfrac{1}{3}\)

Chọn A.
Bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi