A
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SL
0
NT
0
12 tháng 3 2023
\(\dfrac{-2}{5}\cdot\dfrac{4}{7}+\dfrac{-3}{5}\cdot\dfrac{2}{7}+\dfrac{-3}{5}\\ =\dfrac{-2}{5}\left(\dfrac{4}{7}+\dfrac{3}{7}\right)+\dfrac{-3}{5}\\ =-\dfrac{2}{5}+\dfrac{-3}{5}=-1\)
24 tháng 6 2016
C=1+3+32+...+311
3C = 3+32 + 33 +...+311 + 312
=> 3C - C = ( 3+32 + 33 +...+311 + 312 )- (1+3+32 + 33 +...+311) (SỬ DỤNG QUY TẮC DẤU NGOẶC )
3C-C=3+32+33+...+312-1-3-32-33-...-311 (SỬ DỤNG TÍNH CHẤT GIAO HOÁN CỦA PHÉP CỘNG )
3C-C=(3-3)+(32-32)+(33-33)+...+(311-311)+312-1
2C= 312 - 1
=> C = (312 - 1)/2 = 265720=6643.40 ( CHIA HẾT CHO 40 VÌ TÍCH CÓ THỪA SỐ 40)
17 tháng 3 2018
Đề còn thiếu 1 điều kiện nữa là \(n>0\)
Đặt \(A=\frac{4}{5.2!}+\frac{4}{5.3!}+\frac{4}{5.4!}+...+\frac{4}{5.n!}\) ta có :
\(A=\frac{4}{5}\left(\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...+\frac{1}{n!}\right)\)
Để \(A< 0,8\) thì \(\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...+\frac{1}{n!}< 1\)
Đặt \(B=\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+...+\frac{1}{n!}\) ta có :
\(B< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{\left(n-1\right)n}\)
\(B< \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n-1}+\frac{1}{n}\)
\(B< 1-\frac{1}{n}< 1\)
\(\Rightarrow\)\(B< 1\) ( đpcm )
Suy ra : \(A=\frac{4}{5}.B=0,8.B< 0,8\) ( vì \(B< 1\) )
Vậy \(\frac{4}{5.2!}+\frac{4}{5.3!}+\frac{4}{5.4!}+...+\frac{4}{5.n!}< 0,8\)
Chúc bạn học tốt ~
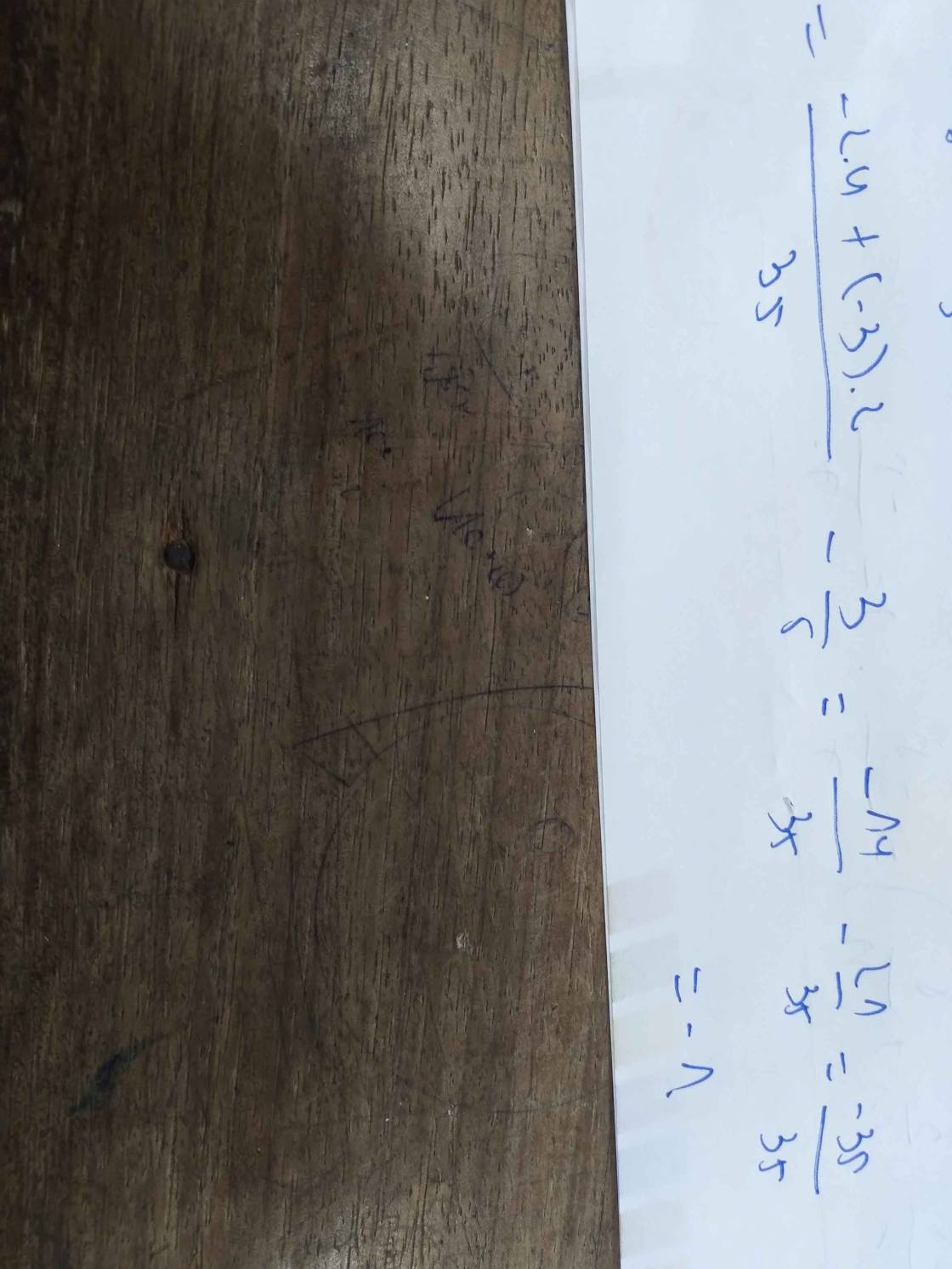
vế trái được viết dưới dạng :
\(\frac{3}{5}.\left(\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+....+\frac{1}{100!}\right)< \frac{3}{5}.\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{99.100}\right)\)
\(=\frac{3}{5}\left(1-\frac{1}{100}\right)< \frac{3}{5}=0,6\)