Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, N(x)=3x+4
Ta có:
\(N\left(x\right)=0\Leftrightarrow3x+4=0\Leftrightarrow3x=-4\Leftrightarrow x=-\frac{4}{3}\)
Vậy \(x=-\frac{4}{3}\) là nghiệm của đa thức N(x) = 3x + 4

Bạn xem lời giải của mình nhé:
Giải:
\(x^2\ge0\forall x\\ 4>0\\ \Rightarrow x^2+4>0\forall x\\ \Rightarrow M_{\left(x\right)}>0\forall x\\ \Rightarrow M_{\left(x\right)}\ne0\forall x\)
Vậy đa thức M(x) vô nghiệm.
Chúc bạn học tốt!![]()
Vì \(^{x^2\ge0}\)
\(\Rightarrow x^2+4\ge4\)
Vậy đa thức trên không có nghiệm

a.
\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)
b.
\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)
c.
\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)
d.
\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)
e.
\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)
g.
\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)

Lời giải:
\(F(x)=\int \frac{x^3+3x^2+3x-1}{x^2+2x+1}dx=\int \frac{x^3+3x^2+3x+1-2}{(x+1)^2}dx\)
\(=\int \frac{(x+1)^3-2}{(x+1)^2}dx\)
\(=\int \left(x+1-\frac{2}{(x+1)^2}\right )dx\)
\(=\int (x+1)dx-2\int \frac{dx}{(x+1)^2}=\int (x+1)dx-2\int \frac{d(x+1)}{(x+1)^2}\)
\(=\frac{x^2}{2}+x+\frac{2}{x+1}+c\)
Vì \(F(1)=\frac{1}{3}\Leftrightarrow \frac{1}{2}+1+\frac{2}{1+1}+c=\frac{1}{3}\)
\(\Leftrightarrow c+\frac{5}{2}=\frac{1}{3}\Leftrightarrow c=\frac{-13}{6}\)
Do đó: \(F(x)=\frac{x^2}{2}+x+\frac{2}{x+1}-\frac{13}{6}\)

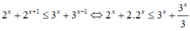
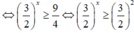
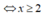
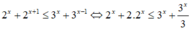

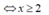
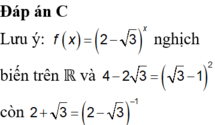
cộng H(x)với G(x)
H(x)+G(x)=(x^3-2x^2+3x-1)+(-x^3+3x^2-3x+3)
=x^3-2x^2+3x-1-x^3+3x^2-3x+3
=x^2+2
mà x^2 lớn hơn hoặc bằng 0
nên x^2+2 lớn hơn 0
suy ra đa thức H(x) và G(x) không có nghiệm chung nào