Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{1.2.3}\) + \(\dfrac{1}{2.3.4}\) + .....+ \(\dfrac{1}{10.11.12}\)
= \(\dfrac{1}{1.2}\) - \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\) - \(\dfrac{1}{3.4}\) +....+ \(\dfrac{1}{10.11}\) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{1.2}\) + (- \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\))+.......+ ( \(-\dfrac{1}{10.11}\) + \(\dfrac{1}{10.11}\)) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{2}\) - \(\dfrac{1}{11.12}\) =\(\dfrac{1}{2}\) - \(\dfrac{1}{132}\) =\(\dfrac{66}{132}\)-\(\dfrac{1}{132}\) =\(\dfrac{65}{132}\) Vì \(\dfrac{33}{132}\) = \(\dfrac{1}{4}\) nên \(\dfrac{65}{132}\) > \(\dfrac{1}{4}\)
Lời giải:
a.
$x=\frac{-5}{6}-\frac{2}{3}=\frac{-3}{2}$
b.
$\frac{2}{3}x=\frac{1}{10}-\frac{1}{2}=\frac{-2}{5}$
$x=\frac{-2}{5}: \frac{2}{3}=\frac{-3}{5}$
c.
$\frac{7}{8}x=\frac{2}{9}-\frac{1}{3}=\frac{-1}{9}$
$x=\frac{-1}{9}: \frac{7}{8}=\frac{-8}{63}$
d.
$\frac{5}{7}: x=\frac{1}{6}-\frac{4}{5}=\frac{-19}{30}$
$x=\frac{5}{7}: \frac{-19}{30}=\frac{-150}{133}$
e.
$(\frac{2}{5}-1\frac{2}{3}):x=\frac{2}{5}+\frac{3}{5}=1$
$\frac{-19}{15}: x=1$
$x=\frac{-19}{15}:1 =\frac{-19}{15}$
f.
$(-\frac{3}{4}+x).2\frac{2}{3}=1$
$\frac{-3}{4}+x=1: 2\frac{2}{3}=\frac{3}{8}$
$x=\frac{3}{8}+\frac{3}{4}=\frac{9}{8}$

\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{10.11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}\)
\(=\dfrac{65}{264}\)
Vậy...

\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\)
\(A=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot...\cdot30\right)^2}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot30}\)
\(A=\dfrac{1\cdot31}{30}=\dfrac{31}{30}\)
Ta có : \(\dfrac{1}{101}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
Do đó :
\(\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{1}{300}+\dfrac{1}{300}..+\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{200}{300}=\dfrac{2}{3}\)
Vậy...

câu b bài 2:
\(\dfrac{1^2}{1\cdot2}\cdot\dfrac{2^2}{2\cdot3}\cdot\dfrac{3^2}{3\cdot4}\cdot\dfrac{4^2}{4\cdot5}\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot\dfrac{4}{5}\)
\(=\dfrac{1}{5}\)
câu a bài 2:
\(\dfrac{1}{1\cdot2\cdot3}+\dfrac{1}{2\cdot3\cdot4}+\dfrac{1}{3\cdot4\cdot5}+...+\dfrac{1}{10\cdot11\cdot12}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{4}-...-\dfrac{1}{12}\)
\(=1-\dfrac{1}{12}=\dfrac{11}{12}\)

* Chứng tỏ
Ta có :\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{98.99.100}\)
= \(\dfrac{1}{1.2.3}.\dfrac{2}{2}+\dfrac{1}{2.3.4}.\dfrac{2}{2}+...+\dfrac{1}{98.99.100}.\dfrac{2}{2}\)
= \(\dfrac{1}{2}.\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+\dfrac{2}{3.4.5}+...+\dfrac{2}{98.99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{98.99}-\dfrac{1}{99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{1.2}+0+0+...+0+\dfrac{-1}{99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{2}+\dfrac{-1}{9900}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{4850}{9900}+\dfrac{-1}{9900}\right)\)
= \(\dfrac{1}{2}.\dfrac{4849}{9900}\)
= \(\dfrac{4849}{19800}\)

Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)

\(2A=\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+\dfrac{2}{3.4.5}+...+\dfrac{2}{18.19.20}\)
\(\Rightarrow2A=\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{18.19}-\dfrac{1}{19.20}\)
\(\Rightarrow2A=\dfrac{1}{1.2}-\dfrac{1}{19.20}< \dfrac{1}{1.2}\)
\(\Rightarrow2A< \dfrac{1}{2}\)
\(\Rightarrow A< \dfrac{1}{4}\) (đpcm)
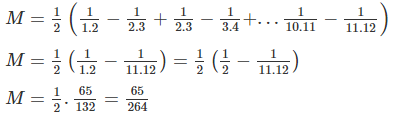
Ta có:
\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}=\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+....+\dfrac{1}{10.11}-\dfrac{1}{11.12}=\dfrac{1}{1.2}-\dfrac{1}{11.12}=\dfrac{1}{2}-\dfrac{1}{132}=\dfrac{65}{132}\)Mà \(\dfrac{65}{132}\ne\dfrac{1}{4}\Rightarrow\) Có thể bạn ghi sai đề thì phải !
ừm dấu = thành dấu < nha, sorry