TH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
31 tháng 1 2019
a) Rút gọn P = 3 Þ giá trị của biểu thức P không phụ thuộc vào giá trị của m.
b) Rút gọn Q = 9 Þ giá trị của biểu thức Q không phụ thuộc vào giá trị của m.
PG
6 tháng 6 2021
a)P=x(2x+1)-x2(x+2)+x3-x+3
P=2x2+x-x3-2x2+x3-x+3
P=(2x2-2x2)+(x-x)+(-x3+x3)+3
P= 0 + 0 + 0 +3
P=3
Vậy giá trị của của biểu thức đã cho không phụ thuộc vào giá trị của biến x
NT
30 tháng 7 2021
a) \(2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]-3\left[\left(x+y\right)^2-2xy\right]\)
\(=2\left(1-3xy\right)-3\left(1-2xy\right)\)
\(=2-6xy-3+6xy=-1\)
\(\Rightarrow\) Giá trị của biểu thức không phụ thuộc vào biến \(x,y\)
b) \(\dfrac{\left(x+5\right)^2+\left(x-5\right)^2}{x^2+25}\)
\(=\dfrac{x^2+10x+25+x^2-10x+25}{x^2+25}\)
\(=\dfrac{2x^2+50}{x^2+25}=\dfrac{2\left(x^2+25\right)}{x^2+25}=2\)
\(\Rightarrow\) Giá trị của biểu thức không phụ thuộc vào biến \(x\)
4 tháng 10 2021
\(A=\left(3x-2\right)\left(2x+3\right)+x\left(x-6\right)-x^2-5x+2020\)
\(=6x^2+9x-4x-6+x^2-6x-x^2-5x+2020\)
\(=6x^2-6x+2014\)
LP
1
19 tháng 9 2021
\(A=\left(x^2-2\right)\left(x^2+x+1\right)-x\left(x^3+x^2-3x-2\right)=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x=2\left(đpcm\right)\)
23 tháng 10 2021
1: \(\left(2x-5\right)\left(2x+5\right)-\left(2x-3\right)^2-12x\)
\(=4x^2-25-4x^2+12x-9-12x\)
=-34
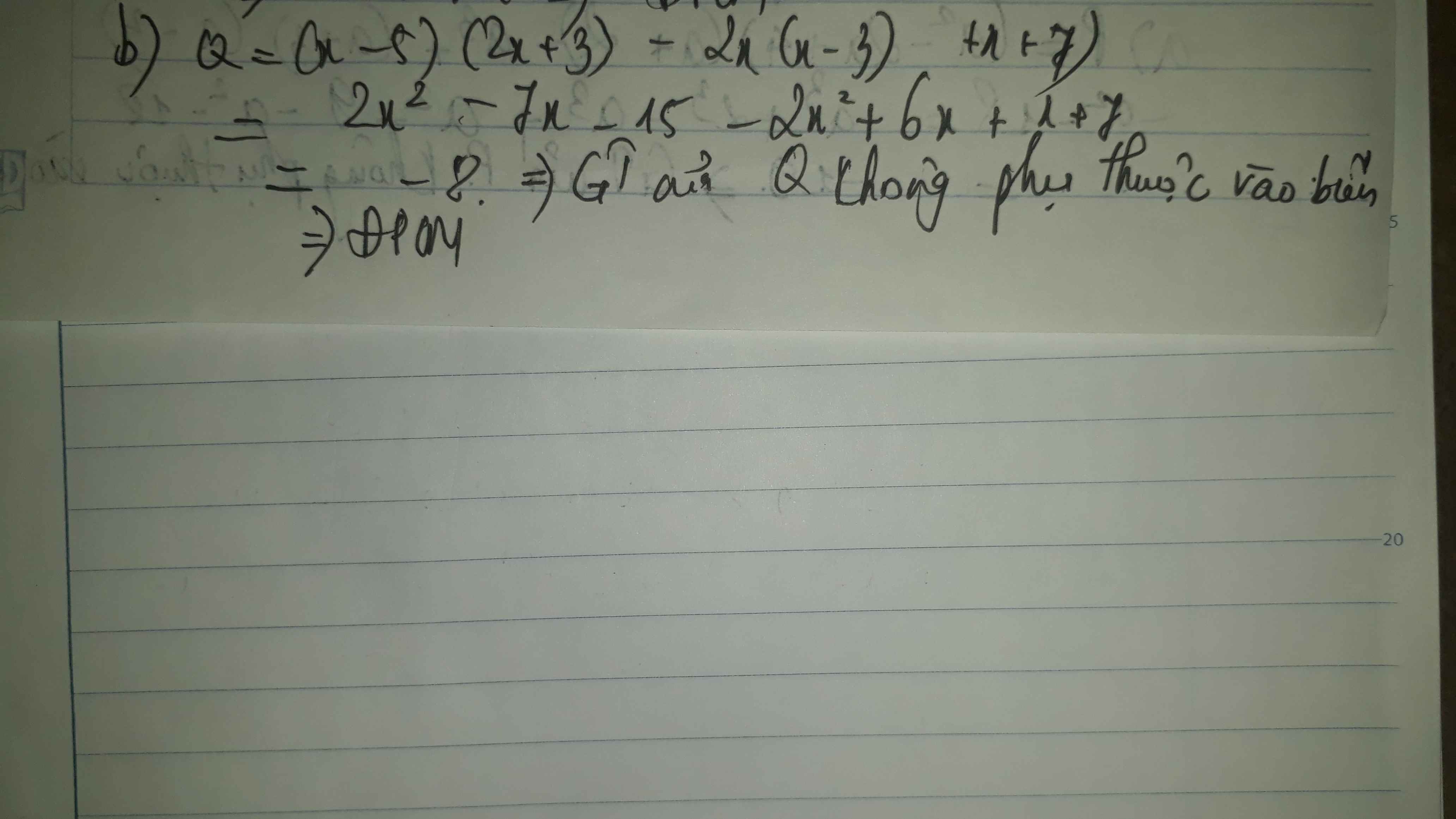
\(x.\left(2x+1\right)-x^2.\left(x+2\right)+\left(x^3-x+3\right)\)
\(=2x^2+x-x^3-2x^2+x^3-x+3\)
\(=\left(-x^3+x^3\right)+\left(2x^2-2x^2\right)+\left(x-x\right)+3\)
\(=3\)
Vậy giá trị của biểu thức trên không phụ thuộc vào biến.
x(2x+1)-x2 (x+2)+(x3-x+3)
=2x2+x-x3-2x2+x3-x+3
=(2x2-2x2)+(x-x)-(x3-x3)+3
=0+0-0+3=3
Vậy biểu thức sau không phụ thuộc vào biến