
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}2x^3+x^2y=3\left(1\right)\\2y^3+xy^2=3\end{matrix}\right.\)
Trừ vế theo vế hai phương trình ta được:
\(2\left(x^3-y^3\right)+\left(x^2y-xy^2\right)=0\)
\(\Leftrightarrow2\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(2x^2+3xy+2y^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\right]=0\left(2\right)\)
Do \(2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\ge0\), đẳng thức xảy ra khi \(x=y=0\)
Thay vào phương trình ta thấy \(x=y=0\) không phải là nghiệm
\(\Rightarrow2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2>0\)
Khi đó \(\left(2\right)\Leftrightarrow x=y\)
\(\left(1\right)\Leftrightarrow2x^3+x^3=3\Leftrightarrow x=y=1\)
\(\Rightarrow x_0^3+y_0^3=2\)

Áp dụng bđt AM - GM:
\(x^3+1+1\ge3x;y^3+1+1\ge3y;z^3+1+1\ge3z;2x+2y+2z\ge6\sqrt[3]{xyz}=6\).
Cộng vế với vế các bđt trên rồi rút gọn ta có đpcm.

![]()
Hệ phương trình tương đương S + P = 11 S P = 30 ⇒ S 11 − S = 30
![]()
Khi S=5 thì P=6 nên x, y là nghiệm của hệ phương trình x + y = 5 x y = 6 ⇔ x = 2 ; y = 3 x = 3 ; y = 2 suy ra hệ có nghiệm (2; 3), (3; 2)
Khi S=6 thì P=5 nên x, y là nghiệm của hệ phương trình x + y = 6 x y = 5 ⇔ x = 1 ; y = 5 x = 5 ; y = 1 suy ra hệ có nghiệm (1; 5), (5; 1).
Đáp án cần chọn là: D


Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12

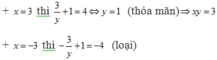

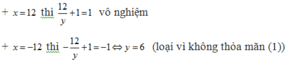
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
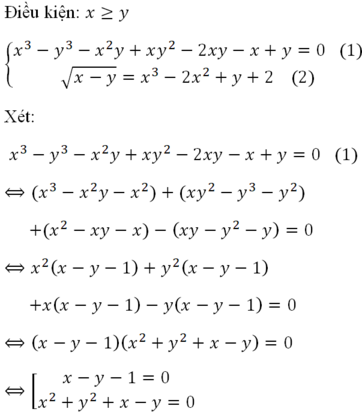

Với x ≥ 0; y ≥ 0 thì x + y ≥ 0
Ta có: x3 + y3 ≥ x2y + xy2
⇔ (x3 + y3) – (x2y + xy2) ≥ 0
⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0
⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0
⇔ (x + y)(x2 – 2xy + y2) ≥ 0
⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)
Dấu « = » xảy ra khi (x – y)2 = 0 ⇔ x = y.