TL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BJ
0
HR
1
P
1
XO
12 tháng 2 2020
Gọi (12n + 5;18n + 7) = d
=> \(\hept{\begin{cases}12n+5⋮d\\18n+7⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(12n+5\right)⋮d\\2\left(18n+7\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}36n+15⋮d\\36n+14⋮d\end{cases}}}\)
=> 36n + 15n - (36n + 14) \(⋮\)d
=> 1 \(⋮\)d
=> d \(\in\)Ư(1)
Vì \(n\inℤ\Rightarrow\hept{\begin{cases}12n+5\inℤ\\18n+7\inℤ\end{cases}\Rightarrow d\inℤ}\)
Khi đó d \(\in\left\{1;-1\right\}\)
=> 12n + 5 ; 18n + 7 là 2 số nguyên tố cùng nhau
=> \(\frac{12n+5}{18n+7}\)là phân số tối giản
NT
1
LG
11
TL
24 tháng 8 2015
gọi d là ƯCLN của 21n+4 và 14n+3
=> 21n+4 chia hết cho d =>2.(21n+4) chia hết cho d
14n+3 chia hết cho d =>3.(14n+3) chia hết cho d
=> (42n+9)-(42n+8) chia hết cho d
=> 42n+9-42n-8 chia hết cho d
=>1 chia hết cho d
=> d thuộc Ư(1)={1}
=> ƯCLN(21n+4;14n+3)=1 => phân số 21n+4/14n+3 là phân số tối giản (ĐPCM)
XB
1
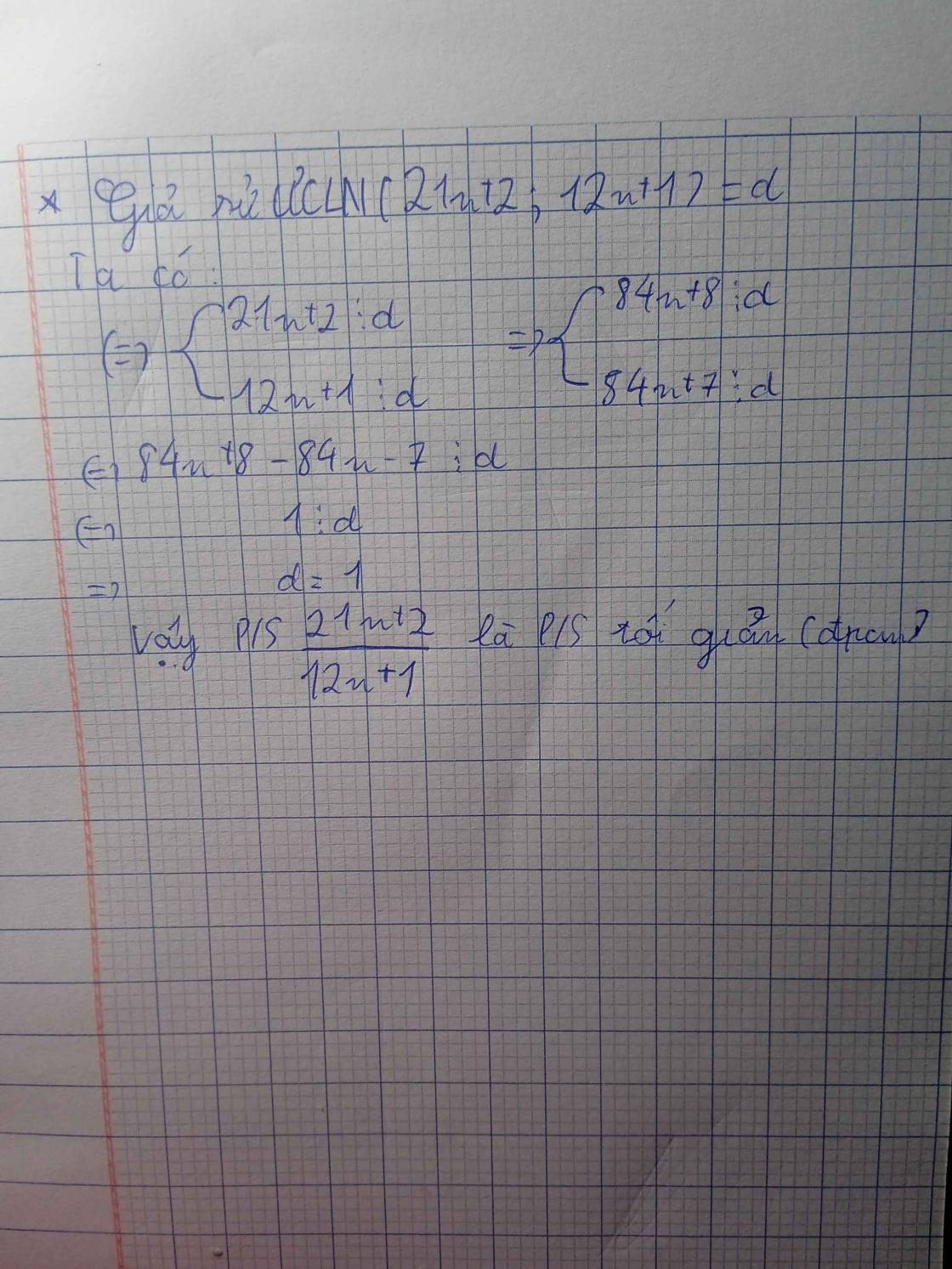
đặt \(ƯCLN_{\left(21n+1;18n+1\right)}=d\)
\(\Rightarrow\hept{\begin{cases}21n+1⋮d\\18n+1⋮d\end{cases}}\)
\(\Rightarrow\left(21n+1\right)-\left(18n+1\right)⋮d\)
\(\Leftrightarrow3n⋮d\)\(\Rightarrow21n⋮d\)
mà \(21n+1⋮d\)
\(\Rightarrow21n+1-21n⋮d\)\(\Leftrightarrow1⋮d\)
\(\Rightarrow d=1\)
do đó phân số 21n+1/18n+1 tối giản với mọi số tự nhiên n
goi d la ƯCLN(21N+1;18N+1)
TA CÓ 18N+1 CHIA HẾT CHO d
21N+1 CHIA HẾT CHO d
=> 126N+7 CHIA HẾT CHO d
126N+6 CHIA HẾT CHO d
=>126N+7-126N-6 CHIA HẾT CHO d
=>1 CHIA HẾT CHO d
=>d=1
VẬY ƯCLN CỦA TỬ VÀ MẪU LÀ 1 =>PHÂN SỐ TỐI GIẢN VỚI MỌI N THUỘC N