Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

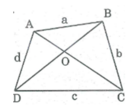
Đặt độ dài a = AB, b = BC, c = CD, d = AD
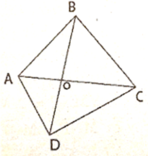
Gọi O là giao điểm 2 đường chéo AC và BD.
* Trong ∆ OAB, ta có:
OA + OB > a (bất đẳng thức tam giác) (1)
* Trong ∆ OCD, ta có:
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c hay AC + BD > a + c (*)
* Trong ∆ ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)
* Trong ∆ OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra:
OA + OB + OC + OD > b + d hay AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
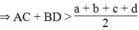
* Trong ∆ ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
* Trong ∆ ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
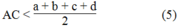
* Trong ∆ ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
* Trong ∆ BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
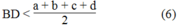
Từ (5) và (6) suy ra: AC + BD < a + b + c + d

Đặt p = AB + BC + CD + DA
Ta có: OA + OD > AD (1)
OA + OB > AB (2)
OB + OC > BC (3)
OC + OD > CD (4)
Cộng vế theo vế (1), (2), (3), (4) ta có:
2(OA + OB + OC + OD) > AB + BC + CD + DA
2(AC + BD) > p
AC + BD > p/2 (*)
Mặt khác: Trong ΔABC có AC < AB + BC (5)
Trong ΔACD có AC < AD + CD (6)
Cộng vế theo vế (5) và (6) ta có:
2AC < AB + BC + CD + DA
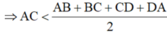
![]()
Tương tự ta cũng có BD < p/2. Suy ra: AC + BC < (p/2) + (p/2)
Hay AC + BD < p (**)
Từ (*) và (**) ta có: (p/2) < AC + BD < p.

- Theo bất đẳng thức tam giác , ta có : \(AO+OB>AB\)
\(OB+OC>BC\)
\(OC+OD>CD\)
\(OD+OA>AD\)
\(\Rightarrow2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\Leftrightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\)
- Tương tự, ta có : \(AC< AB+BC\) ; \(AC< AD+CD\)
\(BD< AB+AD\) ; \(BD< BC+CD\)
\(\Rightarrow2\left(AC+BD\right)< 2\left(AB+BC+CD+AD\right)\Leftrightarrow AC+BD< AB+BC+CD+AD\)
Vậy ta có : \(\frac{AB+BC+CD+AD}{2}< AC+BD< AB+BC+CD+AD\)

Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm)
giao của AC và BD là O.
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC
cổng 4 bất đẳng thức cùng chiề này lại ta có:
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm)
*Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm)
* giao của AC và BD là O.
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC
cổng 4 bất đẳng thức cùng chiề này lại ta có:
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm)

Giả sử tứ giác đó là ABCD , hai đường chéo AC và BD cắt nhau tại O
- Theo bất đẳng thức tam giác, ta có : \(AO+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OD+OA>AD\)
\(\Rightarrow OA+OB+OB+OC+OC+OD+OD+OA>AB+BC+CD+DA\)
\(\Leftrightarrow2\left(AC+BD\right)>AB+BC+CD+AD\Leftrightarrow AC+BD>\frac{AB+BC+CD+AD}{2}\)
- Theo bất đẳng thức tam giác : \(AB+BC>AC\) ; \(AD+DC>AC\); \(AB+AD>BD\) ;
\(BC+CD>BD\)
\(\Rightarrow AB+BC+AD+DC+AB+AD+BC+CD>AC+AC+BD+BD\)
\(\Leftrightarrow2\left(AB+BC+CD+DA\right)>2\left(AC+BD\right)\Leftrightarrow AB+BC+CD+DA>AC+BD\)

Gọi O là giao của AC và BD
AB>AO+BO
AD>AO+DO
BC>BO+CO
DC>DO+CO
=>AB+AD+BC+CD>2(AC+BD)
=>(AC+BD)<P/2
AC<AB+BC
AC<AD+DC
BD<BC+CD
BD<AB+AD
=>2(AC+BD)<2*C ABCD
=>AC+BD<C ABCD

Gọi O là giao điểm của AC và BD.Ta có :
OA + OB > AB , OB + OC > AC ; OC + CD > CD , OD + OA > AD.Cộng từng vế các bất đẳng thức trên rồi chia cho 2 ,ta được \(AC+BD>\frac{AB+BC+CD+AD}{2}\)
Vậy tổng hai đường chéo lớn hơn nửa chu vi
Kết hợp : AC + BD < AB + BC + CD + DA
Vậy \(\frac{AB+BC+CD+AD}{2}< AC+BD< AB+BC< CD+DA\)