Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bài toán có 13 đồng tiền trong đó có 1 đồng bị lỗi không biết nặng hơn hay nhẹ hơn đồng tiền còn lại qua 3 lần cân thăng bằng tìm gia đồng bị lỗi. Lời giải:
-Bỏ 8 đồng tiền vàng vào hai bên cân,mỗi bên 4 đồng,nếu cân thăng bằng,vậy đồng tiền còn lại là giả.
-Nếu 1 trong 2 bên cân nặng hơn bên còn lại,bỏ 4 đồng bên cân nặng xuống,lấy 2 đồng bên cân nhẹ bỏ qua để mỗi cân có 2 đồng.
-Bên nào nhẹ hơn thì bỏ bên còn lại xuống,lấy 1 đồng bên cân nhẹ bỏ vào cân kia,bên nào nhẹ hơn thì đó là đồng tiền vàng giả.
Để biết được đâu là đồng tiền giả chúng ta chỉ cần thực hiện 2 lần cân. Cụ thể như sau:
Lần cân thứ nhất: Các bạn đem 9 đồng tiền chia làm 3 phần mỗi phần sẽ bao gồm 3 đồng tiền vàng. Sau đó chúng ta đem 2 phần bất kỳ lên cân. Phần nào nhẹ hơn chứng tỏ phần đó có chứa đồng vàng giải. Trong trường hợp 2 phần tiền vàng này có trọng lượng bằng nhau thì phần còn lại (phần không được cân) là phần có chứa đồng vàng giả.Lần cân thứ 2: Ở lần cân thứ nhất chúng ta đã xác nhận được phần có chứa 1 đồng tiền giả. Tương tự như trên chúng ta thực hiện cân 2 đồng tiền bất kỳ nếu đồng vàng nào nhẹ hơn thì đồng đó là tiền giả. Trong trường hợp 2 đồng vàng được cân bằng nhau thì đồng tiền không cân là giả.
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
\(y'=3x^2-6mx+3\left(3m-4\right)=3\left[x^2-2mx+3m-4\right]\)
Xét \(f\left(x\right)=x^2-2mx+3m-4\)
\(\Delta'=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\) ;\(\forall m\)
a. Để hàm số đồng biến trên khoảng đã cho
\(\Leftrightarrow x^2-2mx+3m-4\ge0\) ; \(\forall x\le1\)
\(\Leftrightarrow1\le x_1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)\ge0\\\dfrac{x_1+x_2}{2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1\ge0\\x_1+x_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-4-2m+1\ge0\\2m>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge3\\m>1\end{matrix}\right.\) \(\Rightarrow m\ge3\)
b.
Để hàm đồng biến trên khoảng đã cho
\(\Leftrightarrow x^2-2mx+3m-4\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-4-4m+4\ge0\\2m< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le0\\m< 2\end{matrix}\right.\) \(\Rightarrow m\le0\)
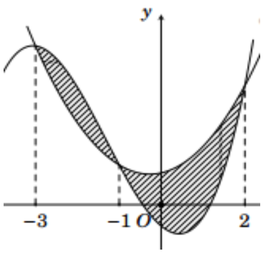
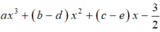
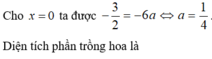
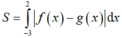
ôi ài thế bạn cho bài dễ hơn đi
:v