Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số f(x) = 3 x 5 + 15x - 8 là hàm số liên tục và có đạo hàm trên R.
Vì f(0) = -8 < 0, f(1) = 10 > 0 nên tồn tại một số x0 ∈ (0;1) sao cho f(x0) = 0, tức là phương trình f(x) = 0 có nghiệm.
Mặt khác, ta có y' = 15 x 4 + 5 > 0, ∀x ∈ R nên hàm số đã cho luôn đồng biến. Vậy phương trình đó chỉ có một nghiệm.

Chọn D.
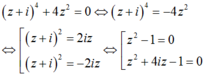
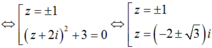
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.

Xét hàm số vế trái \(f\left(x\right)=x^3-3x+c\)
Ta có: \(f'\left(x\right)=3x^2-3=3\left(x^2-1\right)\)
Hàm số liên tục trên toàn trục số và trên khoảng (0;1) thì \(f'\left(x\right)< 0\) nên hàm số nghịch biến trên [0;1]. Vậy phương trình f(x)=0 không thể có hai nghiệm trên [0; 1].

Gọi \(x_1,x_2\) là các nghiệm phương trình và \(r=\left|x_2\right|=\left|x_2\right|\) Khi đó :
\(\frac{p^2}{q^2}=\frac{\left(x_1+x_2\right)^2}{x_1x_2}=\frac{x_1}{x_2}+\frac{x_2}{x_1}+2=\frac{x_1\overline{x_2}}{r^2}+\frac{x_2\overline{x_1}}{r^2}+2=2+\frac{2}{r^2}Re\left(x_1\overline{x_2}\right)\)
Là số thực, hơn nữa :
\(Re\left(x_1\overline{x_2}\right)\ge-\left|x_1\overline{x_2}\right|=-r^2\)
Do đó \(\frac{p^2}{q^2}\ge0\)
vậy \(\frac{p}{q}\) là một số thực


Đặt \(t=2^x\left(t>0\right)\), xét hàm số \(F\left(t\right)=\frac{a}{3}t^3+\frac{b}{3}t^2+ct\) khả vi liên tục trên \(\left(0;+\infty\right)\) và \(F\left(1\right)-F\left(0\right)=\frac{a}{3}+\frac{b}{2}+c=0\)
Theo định lí Laggange thì tồn tại ít nhất 1 số \(k\in\left(0;1\right)\) sao cho :
\(F'\left(k\right)=ak^2+bk+c=0\)
Do đó \(x=\log_2k\) là nghiệm của phương trình đã cho
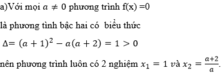
Hàm số f(x) = 3 x 5 + 15x - 8 là hàm số liên tục và có đạo hàm trên R.
Vì f(0) = -8 < 0, f(1) = 10 > 0 nên tồn tại một số x 0 ∈ (0;1) sao cho f( x 0 ) = 0, tức là phương trình f(x) = 0 có nghiệm.
Mặt khác, ta có y' = 15 x 4 + 5 > 0, ∀ x ∈ R nên hàm số đã cho luôn đồng biến. Vậy phương trình đó chỉ có một nghiệm.