Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cạnh hình vuông dài:
96 : 4 = 24 (m)
Diện tích hình vuông hay diện tích hình thang là:
24 x 24 = 576 ( m 2 )
a) Chiều cao hình thang là:
576 : 36 = 16 (m)
b) Tổng hai đáy hình thang là:
36 x 2 = 72 (m)
Đáy bé dài: (72 – 10 ) : 2 =31 (m)
Đáy lớn dài: 31 + 10 = 41 (m)
Đáp số: a) 16m ;
b) 41m, 31m.

Cạnh hình vuông dài:
96 : 4 = 24 (m)
Diện tích hình vuông hay diện tích hình thang là:
24 x 24 = 576 (m2)
Tổng hai đáy hình thang là:
36 x 2 = 72 (m)
Đáy bé dài: (72 – 10 ) : 2 =31 (m)
Đáy lớn dài: 31 + 10 = 41 (m)

diện tích hình thang = tổng độ dài 2 đáy nhân với chiều cao chia 2 (cùng một đơn vị đo)
Muốn tính diện tích hình thang :
"đáy lớn đáy bé mang cộng vào
cộng vào nhân với chiều cao
chia đôi lấy nửa thế nào cũng ra"
Diện tích hình thang bằng tổng độ dài đáy nhân với chiều cao ( cùng đơn vị đo) rồi chia cho 2
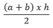
đó là một dạng biến đổi của hình tam giác
MỞ SÁCH GIÁO KHOA TOÁN 5 S HÌNH THANG Í CÓ CÁI HÌNH ĐẤY
nhớ tick nhe
Giả sử hình thang ABCD có đáy dài bằng AB, đáy ngắn bằng CD, chiều cao hình thang bằng h. Ta cần chứng minh rằng diện tích hình thang ABCD bằng:
S = [(AB + CD) x h] / 2
Để bằng chứng cho công thức này, chúng ta có thể sử dụng phương pháp tính diện tích của hình thang như sau:
Bước 1: Vẽ đường chéo AC.
Bước 2: Tính diện tích hai tam giác ACD và ABC.
Diện tích tam giác ACD: S1 = (AC x h) / 2
Diện tích tam giác ABC: S2 = (AC x h) / 2
Bước 3: Tổng diện tích hai tam giác trên là diện tích hình thang ABCD.
S = S1 + S2 = [(AC x h) / 2] + [(AC x h) / 2] = AC x h
Bước 4: Áp dụng định lí Pytago vào tam giác vuông ACD, ta được:
AC^2 = AD^2 + CD^2
AC = √(AD^2 + CD^2)
Bước 5: Thay AC vào công thức tính diện tích, ta có:
S = AC x h = √(AD^2 + CD^2) x h
S = [(AB + CD) x h] / 2
Do đó, ta đã chứng minh rằng diện tích hình thang bằng tổng độ dài hai đấy nhân với chiều cao cùng một đơn vị đo rồi chia cho hai.