Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có:
VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab
= a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2
= (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có:
VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab
= a2 + (2ab – 4ab) + b2
= a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.

\(\left(a+b\right)^2-4ab\)
\(=a^2+2ab+b^2-4ab\)
\(=a^2-2ab+b^2\)
\(=\left(a-b\right)^2=VT\left(đpcm\right)\)

Bài giải:
a) (a + b)2 = (a – b)2 + 4ab
- Biến đổi vế trái:
(a + b)2 = a2 +2ab + b2 = a2 – 2ab + b2 + 4ab
= (a – b)2 + 4ab
Vậy (a + b)2 = (a – b)2 + 4ab
- Hoặc biến đổi vế phải:
(a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + 2ab + b2
= (a + b)2
Vậy (a + b)2 = (a – b)2 + 4ab
b) (a – b)2 = (a + b)2 – 4ab
Biến đổi vế phải:
(a + b)2 – 4ab = a2 +2ab + b2 – 4ab
= a2 – 2ab + b2 = (a – b)2
Vậy (a – b)2 = (a + b)2 – 4ab
Áp dụng: Tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4 . 12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4 . 3 = 400 + 12 = 412
CMR: (a + b)2 = (a - b)2 + 4ab
(a - b)2 = (a + b)2 - 4ab
Ta có: (a + b)2 = a2 + 2ab + b2
= a2 +2ab + b2 - 2ab +2ab
= a2 - 2ab + b2 + 2ab +2ab
= (a - b)2 +4ab
Ta có: (a - b)2 = a2 - 2ab + b2
= a2 - 2ab + b2 + 2ab - 2ab
= a2 + 2ab + b2 - 2ab - 2ab
= (a + b)2 - 4ab
Áp dụng:
a) Tính (a - b)2 , biết a + b = 7 và a.b = 12
Ta có: (a - b)2 = (a + b)2 - 4ab
= 72 - 4.12
= 49 - 48
Vậy (a - b)2 = 1
b) Tính (a + b)2 , biết a - b = 7 và a.b = 3
Ta có: (a + b)2 = (a - b)2 + 4ab
= 72 + 4.3
= 49 + 12
Vậy ( a + b)2 = 61


(a+b)2=(a-b)2+4ab
(a+b)2=a2-2ab+b2+4ab
a2+b2+2ab
=(a+b)2
==> (a+b)2=(a-b)2+4ab
(a-b)2=(a+b)2-4ab
a+2ab+b2-4ab
a+b2-2ab
=(a-b)2
==> (a-b)2=(a+b)2-4ab
Áp dụng:
a) (a-b)2=72-4.12
(a-b)2=49-48=1
b) (a+b)2=122+4.23
(a+b)2=144+92=236
Xong!!! Đánh mỏi tay v :V

Mình nhầm
a)Ta có: (a+b)2=a2+2ab+b2=a2-2ab+4ab+b2=(a2-2ab+b2)+4ab=(a-b)2+4ab
=>(a+b)2=(a-b)2+4ab(1)
b)Ta có: (a-b)2=a2-2ab+b2=a2+2ab-4ab+b2=(a2+2ab+b2)-4ab=(a+b)2-4ab
=>(a-b)2=(a+b)2-4ab(2)
Áp dụng (1) và (2) ta có:
(a-b)2=(a-b)2-4ab=72-4.12=49-48=1
(a+b)2=(a-b)2+4ab=202+4.3=400+12=412
Vậy (a-b)2=1
(a+b)2=412
1)
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab\)
ta có \(\left(a+b\right)^2=a^2+2ab+b^2\left(1\right)\)
\(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab=a^2+2ab+b^2\left(2\right)\)
so sánh ta thấy 1 = 2
\(\Rightarrow\left(a+b\right)^2=\left(a-b\right)^2+4ab\left(đpcm\right)\)
cái thứ 2 tương tự
2) \(\left(a-b\right)^2=\left(a+b\right)^2-4ab\)= 72-4*12=1
(a+b)2=(a-b)2+4ab = 202+4*3=412
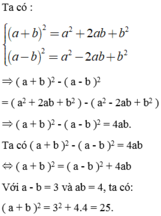
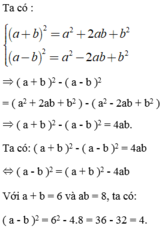
ta có :a) (a-b)2+4ab=a2-2ab+b2+4ab=a2+2ab+b2=(a+b)2 b) (a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2=(a-b)2 Áp dụng: (a-b)2=(a+b)2-4ab=72-4.12=1 (a+b)2=(a-b)2+4ab=202+4.3=412
GG