TD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
1
DD
Đoàn Đức Hà
Giáo viên
23 tháng 6 2021
\(x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)+3\left(x+y\right)^2-6xy+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x+y+2\right)\left(\left(x+y\right)^2+x+y+2\right)-3xy\left(x+y+2\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left(x^2+y^2+2xy+x+y+2-3xy\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left[\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2+2\right]=0\)
\(\Leftrightarrow x+y+2=0\)
\(\Leftrightarrow x+y=-2\)
\(M=\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}=\frac{4}{-2}=-2\)
Dấu \(=\)khi \(x=y=-1\).
CM
12 tháng 10 2017
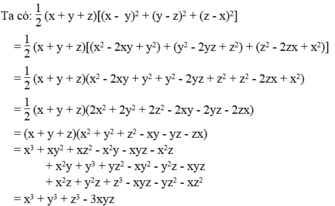
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
PT
1
CM
13 tháng 11 2018
Đ ặ t x = a 3 y = b 3 z = c 3 , v ì x , y , z > 0 x y z = 1 = > a , b , c > 0 a b c = 1
Ta có: x + y + 1 = a 3 + b 3 + 1 = ( a + b ) ( a 2 − a b + b 2 ) + 1 ≥ ( a + b ) a b + 1 = a b ( a + b + c ) = a + b + c c
Do đó: 1 x + y + 1 ≤ c a + b + c
Tương tự ta có: 1 y + z + 1 ≤ a a + b + c 1 z + x + 1 ≤ b a + b + c
Cộng 3 bất đẳng thức trên theo vế ta có đpcm
CM
7 tháng 10 2018
x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0
AH
Akai Haruma
Giáo viên
8 tháng 10 2021
Lời giải:
a. Xét hiệu:
$x^3+y^3-xy(x+y)=(x^3-x^2y)-(xy^2-y^3)=x^2(x-y)-y^2(x-y)$
$=(x-y)(x^2-y^2)=(x-y)^2(x+y)\geq 0$ với mọi $x,y\geq 0$
$\Rightarrow x^3+y^3\geq xy(x+y)$
Dấu "=" xảy ra khi $x=y$
b.
Áp dụng BĐT phần a vô:
$x^3+y^3\geq xy(x+y)$
$\Rightarrow x^3+y^3+1\geq xy(x+y)+1=xy(x+y)+xyz=xy(x+y+z)$
$\Rightarrow \frac{1}{x^3+y^3+1}\leq \frac{1}{xy(x+y+z)}=\frac{xyz}{xy(x+y+z)}=\frac{z}{x+y+z}$
Hoàn toàn tương tự với các phân thức còn lại suy ra:
$\text{VT}\geq \frac{z}{x+y+z}+\frac{x}{x+y+z}+\frac{y}{x+y+z}=1$
Ta có đpcm
Dấu "=" xảy ra khi $x=y=z=1$
CM
19 tháng 11 2018
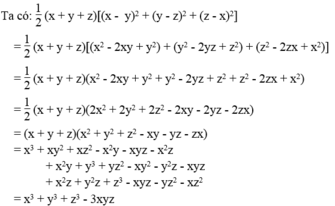
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
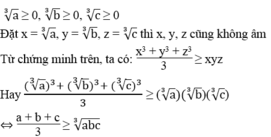
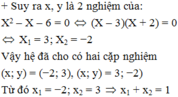
CMR: \(\frac{1}{x}+\frac{1}{y}\le2\) biết \(^{x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0}\) và xy>0
tôi quên mât CMR: 1/x+1/y<=-2