K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
Lời giải:
1.
Xét tam giác $BHA$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}\Rightarrow BA^2=BH.BC$
Tương tự, ta cũng cm được: $\triangle CHA\sim \triangle CAB$ (g.g)
$\Rightarrow CA^2=CH.CB$
Do đó:
$CA^2+CB^2=BH.BC+CH.CB=BC(BH+CH)=BC.BC=BC^2$
(đpcm)
b. Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{AH}=\frac{HA}{HC}$
$\Rightarrow AH^2=BH.CH$
c.
$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}$
$=\frac{BC^2}{AB^2.AC^2}=(\frac{BC}{AB.AC})^2=(\frac{BC}{2S_{ABC}})^2$
$=(\frac{BC}{AH.BC})^2=\frac{1}{AH^2}$
.d. Hiển nhiên theo công thức diện tích.
21 tháng 4 2017
Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.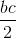
(1)
SGHIK= (b+c)2 = Sa + 4.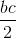 (2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
PQ
0
PQ
0
CM
11 tháng 6 2017
Gọi a (a ∈N*) là số người đang học ở trường đại học của Py-ta-go.
Số người đang học toán là a/2
Số người đang học nhạc là a/4 .
Số người đang suy nghĩ là a/7
Ngoài ra còn có 3 người phụ nữ nên ta có phương trình:
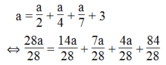
⇔ 28a = 14a + 7a + 4a + 84
⇔ 28a – 25a = 84
⇔ 3a = 84
⇔ a = 28 (thỏa)
Vậy trường đại học của Py-ta-go có 28 người.
17 tháng 6 2017
Sao cậu không tra trên google
Các cách chứng minh định lý pytago là :
Link :
www.bachkhoatrithuc.vn - Các cách chứng minh định lý Pitago,
17 tháng 6 2017
Định lý có thể chứng minh bằng phương pháp đại số khi sử dụng 4 tam giác vuông bằng nhau có các cạnh a, b và c, các tam giác này được sắp xếp thành một hình vuông lớn có cạnh là cạnh huyền c. Các tam giác bằng nhau có diện tích , khi đó hình vuông nhỏ bên trong có cạnh là b − a và diện tích là (b − a)2.
đây là ngử văn????? Khó wa trời
khó ghê