Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Làm phần a thôi,b tự làm mớ!
a)a+b=2005.
Vì 2005 là số lẻ nên a chẵn hoặc b lẻ(không giảm tính tổng quát)
a chẵn a có dạng 2k.
2.k.b=5749
Vế trái chia hết cho 2 mà 5749 lẻ nên ko có.
Học tốt^^
minh chi biet la a ko vi so le ma chia so le thi se ra so chan
minh chac chan a la 0

b: Gọi số bị trừ là x
Số trừ là x-98
Theo đề, ta có: \(x\left(x-98\right)=1998\)
\(\Leftrightarrow x^2-98x-1998=0\)
mà x nguyên
nên \(x\notin\varnothing\)

Gọi 2 số tự nhiên đó lần lượt là a và b \(\left(a,b\in N\text{*}\right)\)
Theo đề ta có:
\(\begin{cases}a-b=2016\left(1\right)\\ab=20162018\left(2\right)\end{cases}\)\(\left(1\right)\Leftrightarrow a=2016+b\)
Thay vào (2) ta có:
\(\left(2016+b\right)b=20162018\)
Bấm máy ta có không có a,b nào thỏa mãn



a) x2-y2=45 =>(x-y)(x+y)=45. Vì x,y là các số tự nhiên và x-y<x+y nên ta có thể viết:
(x-y)(x+y)=3.15 hay (x-y)(x+y)=5.9
=>x-y=3 và x+y=15 hay x-y=5 và x+y=9.
=>x=9 và y=6 (đều loại) hay x=7 và y=2 (đều thỏa mãn).
- Vậy x=7, y=2.
b) - Sửa lại đề: S=1+3+32+33+...+330.
=(1+3+32)+(32+33+34+35)+...+(327+328+329+330).
=13+32(1+3+32+33)+...+327(1+3+32+33)
=13+32.40+...+327.40
=13+40.(32+...+327) chia 5 dư 3.
- Mà các số chính phương chỉ có chữ số tận cùng là 0.1.4.5.6.9 nên số chính phương chia 5 dư 0;1;4.
- Vậy S không phải là số chính phương.
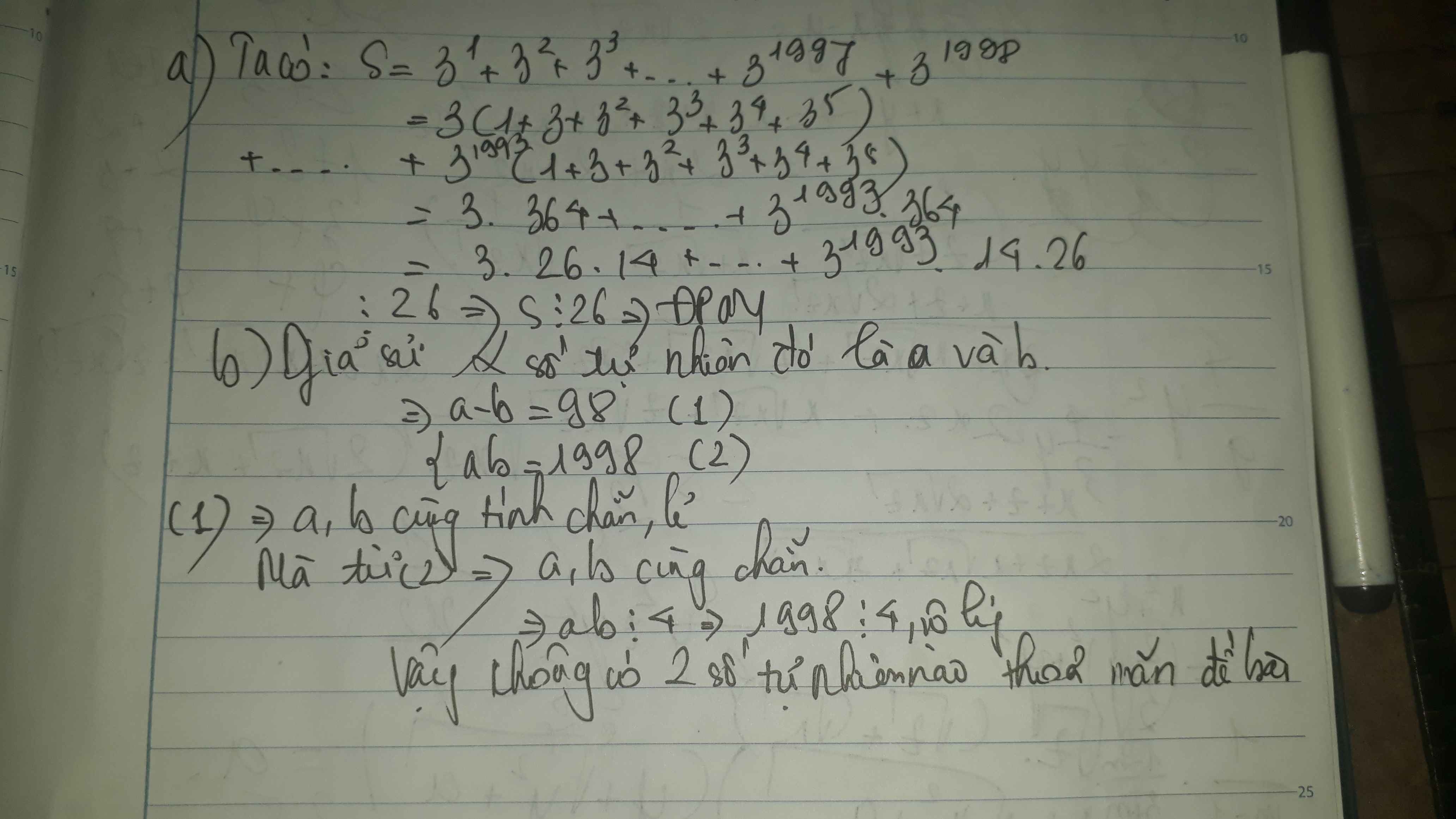
Ta có:
(x-y).(x+y)=x2+y2
=> x2+xy - yx +y2=x2+y2
=>x2+y2=x2+y2
=> (x-y).(x+y)=x2+y2(đpcm)
Chứng minh công thức
Ta có \(\left(x-y\right)\left(x+y\right)=x\left(x+y\right)-y\left(x+y\right)=x^2+xy-xy+y^2=x^2-y^2\)