LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 8 2021
*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3
NT
2
19 tháng 12 2016
Ta có: 20162016 + 20162017 = 20162016.(1+2016) = 20162016 . 2017 chia hết chi 2017
19 tháng 12 2016
Giả sử 20162016 + 20162017 không chia hết cho 2017
Ta có : 20162 = 4064256 = 2015 x 2017 + 1
=> 20162 = 1 ( mod 2017 )
=> (20162)^1008 = 11008 ( mod 2017 )
=> 20162016 = 1 ( mod 2017 )
Ta lại có : 20162016 x 2016 = 1 x 2016 ( mod 2017 )
=> 20162017 = 2016 ( mod 2017 )
Nên 20162016 + 20162017 = 0 ( mod 2017 )
Vậy điều đã giả sử là sai
=> 20162016 x 20162017 chia hết cho 2017 .
mình nha . Yêu , chúc bạn học thật tốt
HN
3
FM
1 tháng 10 2018
Ta có: \(2^{17}+2^{14}\)
\(=2^{14}\left(2^3+1\right)=2^{14}\times9⋮9\)
\(15^3-25^2\)
\(=3^3.5^3-5^4\)
\(=5^3\left(27-5\right)=5^3.2.11⋮11\)
1 tháng 10 2018
\(2^{17}+2^{14}=2^{14}\left(2^3+1\right)=2^{14}\cdot9\Rightarrow2^{17}+2^{14}⋮9\)
VV
0
BH
16 tháng 7 2016
Ta có:
\(3^{2016}+3^{2015}-3^{2014}=3^{2014}\left(3^2+3-1\right)=3^{2014}.11\) chia hết cho 11
Vậy 32016+32015-32014 chia hết cho 11 (đpcm)
--------------------------
Ta có:
- \(36^{36}-9^{10}=4^{36}.9^{36}-9^{10}=9^{10}\left(4^{36}.9^{26}-1\right)=\) chia hết cho 9 (1)
- \(36^{36}-9^{10}=\left(...6\right)-\left(...1\right)=\left(...5\right)\) chia hết cho 5 (2)
Vì 3636 có tận cùng là 6, 910 có tận cùng là 1 => 3636-910 có tận cùng là 5 [ phần này mình chỉ nói thêm thôi nhé ]
Từ (1),(2) và (5;9)=1 =>3636-910 chia hết cho 5.9=45 (đpcm)
16 tháng 7 2016
9. \(3^{2016}+3^{2015}-3^{2014}=3^{2014}\left(3^2+3-1\right)\)
\(=3^{2014}.11⋮11\)
Vậy \(3^{2016}+3^{2015}-3^{2014}\) chia hết cho 11
KN
16 tháng 7 2016
Mình chỉ làm được cái thứ 2 thôi..thông cảm nhé:
36^36 - 9^10 chia hết cho 9 (1) (vì 36^36 và 9^10 đều chia hết cho 9)
36^36 tận cùng là 6 (số tận cùng bằng 6 nâng lên luỹ thừa n (n nguyên dương) thì kết quả cũng tận cùng là 6)
9^10 tận cùng là 1 (9 luỹ thừa m với m chẵn luôn tận cùng là 1)
---> 36^36 - 9^10 tận cùng là 5 và do đó nó chia hết cho 5 (2)
Vì 5 và 9 là 2 số nguyên tố cùng nhau nên từ (1),(2) ---> 36^36 - 9^10 chia hết cho 45.
VA
16 tháng 7 2016
9) Ta có :
32016 + 32015 - 32014 = 32014 . (32 + 3 - 1) = 32014 . (9 + 3 - 1) = 32014 . 11 chia hết cho 11 (ĐPCM)
Tớ chỉ làm đc phần 9 thui ^_^
NT
1
HH
8 tháng 9 2017
a)
= 2 ( 1 + 2) + 22(1 +2) +.........+ 2201591 +2)
= 3( 2 + 22 +........+ 22015) nên chia hết cho 3
b)
= 2( 1 + 2 + 22) + 23( 1 + 2 +22) +......+ 22014( 1 + 2 +22)
= 7( 2 + 23 + .........+ 22014) nên chia hết cho 7
F
1
16 tháng 5 2020
Gọi 2016 số nguyên đấy là: \(a_1;a_2;a_3;...;a_{2016}\)
Ta có: \(a_i^3-a_i=a_i\left(a_i^2-1\right)=a_i\left(a_i-1\right)\left(a_i+1\right)⋮6\) với i là số bất kì từ 1 đến 2016
( 3 số tự nhiên liên tiếp vừa chia hết cho 2 vừa chia hết cho 3 nên chia hết cho 6 )
=> \(\left(a_1^3+a_2^3+a_3^3+...+a_{2016}^3\right)-\left(a_1+a_2+a_3+...+a_{2016}\right)\)
\(\left(a_1^3-a_1\right)+\left(a_2^3-a_2\right)+\left(a_3^3-a_3\right)+...+\left(a_{2016}^3-a_{2016}\right)⋮6\)
mà \(a_1+a_2+a_3+..+a_{2016}=2016⋮6\)
=> \(a_1^3+a_2^3+a_3^3+..+a_{2016}^3⋮6\)
NM
1
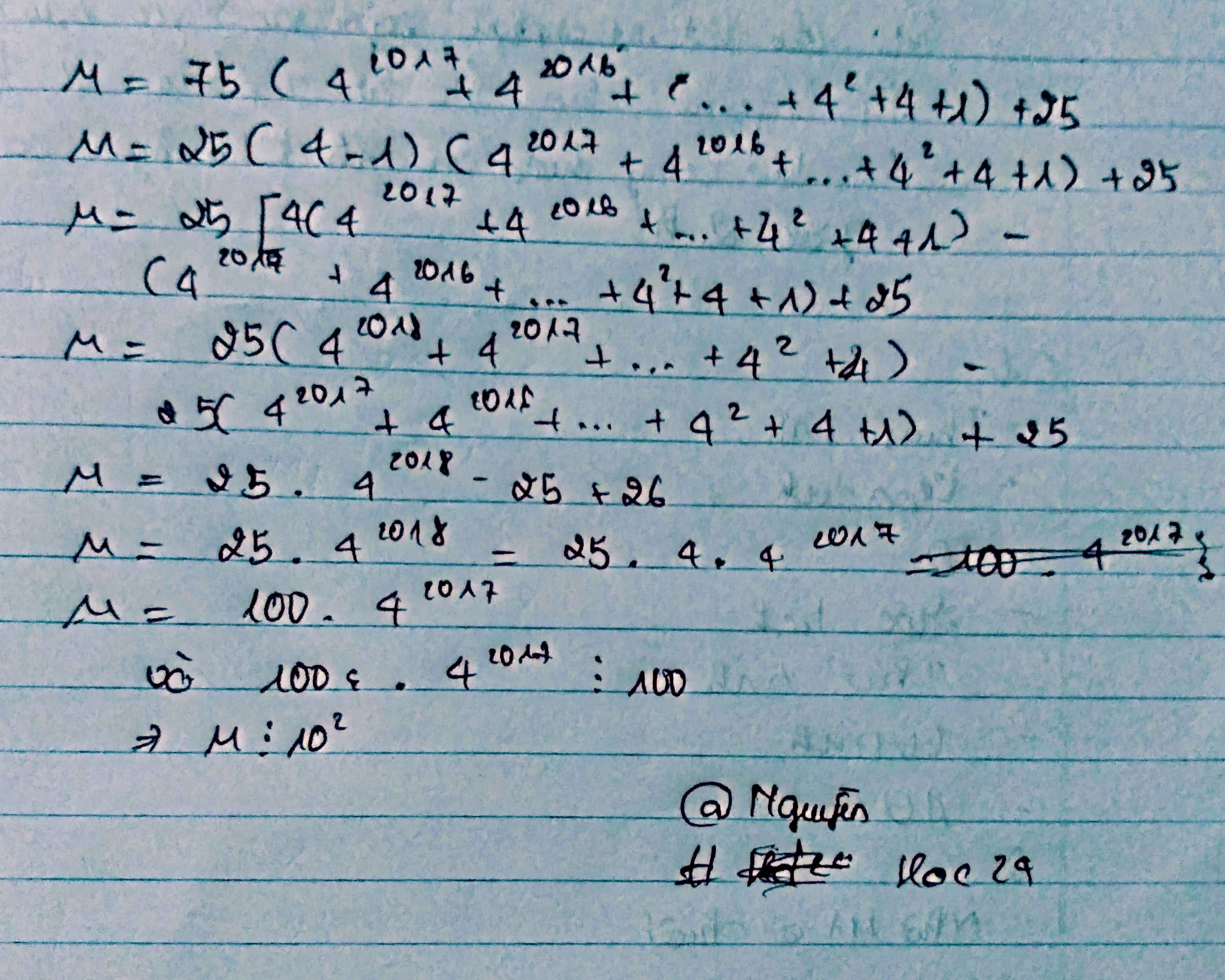
Ta có:
2^100(2^11-2^5)=2^100 x 2^5 x (2^6-1)=2^100 x (2^5 x 63)=2^100 x 2016 suy ra chia hết 2016