DH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 5 2016
Xét hàm số : \(f_n\left(x\right)=e^x-1-x-\frac{x^2}{2}-.......-\frac{x^n}{n!}\)
Ta sẽ chứng minh \(f_n\left(x\right)\ge0\) (*) với mọi \(x\ge;n\in N\)
* Với \(n=1:f_1\left(x\right)=e^x-1-x\Rightarrow f_1'\left(x\right)=e^x-1\ge0\) và \(f'\left(x\right)=0\) khi x = 0
\(\Rightarrow\) Hàm số \(f_1\left(x\right)\) đồng biến với \(x\ge0\Rightarrow f_1\left(x\right)\ge f_1\left(0\right)=0\)
Vậy (*) đúng với n = 1
* Giả sử (*) đúng với n = k hay \(f_k\left(x\right)\ge0\), ta cần chứng minh (*) đúng với \(n=k+1\) hay \(f_{k+1}9x=e^x-1-x-\frac{x^2}{2}-...-\frac{x^k}{k!}-\frac{x^{k+1}}{\left(k+1\right)!}\ge0\)
Thật vậy :
\(f_{k+1}'\left(x\right)=e^x-1-x-\frac{x^k}{k!}=f_k\left(x\right)\ge0\) (theo giả thiết quy nạp và \(f'_{k+1}\left(0\right)\ge f_{k+1}\left(0\right)=0\)khi \(x=0\)
\(\Rightarrow\) hàm số \(f_{k+1}\left(x\right)\) đồng biến với mọi \(x\ge0\Rightarrow f_{k+1}\left(x\right)\ge f_{k+1}\left(0\right)=0\) Vậy (*) đúng với n = k+1
Theo phương pháp quy nạp \(\Rightarrow e^x\ge1+x+\frac{x^2}{2}+..+\frac{x^n}{n!}\) với mọi \(x\ge0;n\in N\)
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 1:
Vì $a\geq 1$ nên:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}=a+\sqrt{(a-1)^2+4}+\sqrt{a-1}\)
\(\geq 1+\sqrt{4}+0=3\)
Ta có đpcm
Dấu "=" xảy ra khi $a=1$
AH
Akai Haruma
Giáo viên
29 tháng 5 2021
Bài 2:
ĐKXĐ: x\geq -3$
Xét hàm:
\(f(x)=x(x^2-3x+3)+\sqrt{x+3}-3\)
\(f'(x)=3x^2-6x+3+\frac{1}{2\sqrt{x+3}}=3(x-1)^2+\frac{1}{2\sqrt{x+3}}>0, \forall x\geq -3\)
Do đó $f(x)$ đồng biến trên TXĐ
\(\Rightarrow f(x)=0\) có nghiệm duy nhất
Dễ thấy pt có nghiệm $x=1$ nên đây chính là nghiệm duy nhất.
LT
1
17 tháng 5 2016
\(e^x\ge x+1\) với mọi \(x\in R\) \(\Leftrightarrow e^x-x-1\ge0\) với mọi \(x\in R\)
Xét hàm số \(f\left(x\right)=e^x-x-1\) với mọi \(x\in R\)
Ta có : \(f'\left(x\right)=e^x-1=0\Leftrightarrow x=0\)
và : \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\left(e^x-x-1\right)=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\left(e^x-x-1\right)=+\infty\)
Xét bảng biến thiên :
Từ bảng biến thiên ta có : \(f\left(x\right)\ge0\) với mọi \(x\in R\)
hay : \(e^x-x-1\ge0\) với mọi \(x\in R\)
=> Điều phải chứng minh
CM
8 tháng 8 2018
Xét hàm số h(x) trên [0; + ∞ )
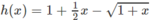
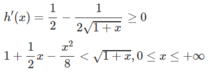
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
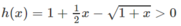
Hay
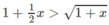
Xét hàm số trên f(x) trên [0; + ∞ );
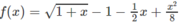
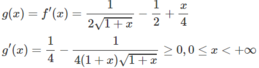
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
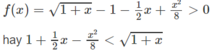
Với mọi 0 < x < + ∞
PT
1
CM
10 tháng 7 2017
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);
x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
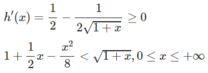
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
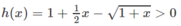
Hay
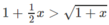
Xét hàm số trên f(x) trên [0; + ∞ );
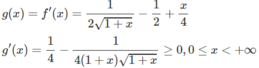
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
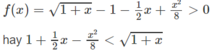
Với mọi 0 < x < + ∞ .
PT
1
CM
3 tháng 3 2019
Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ =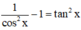 
> 0 với ∀ x ∈ R.
⇒ hàm số đồng biến trên khoảng (0; π/2)
⇒ f(x) > f(0) = 0 với ∀ x > 0
hay tan x – x > 0 với ∀ x ∈ (0; π/2)
⇔ tan x > x với ∀ x ∈ (0; π/2) (đpcm).
NY
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2020
\(\Leftrightarrow\left|cosx\right|\ge cos^2x\)
\(\Leftrightarrow\left|cosx\right|-\left|cosx\right|^2\ge0\)
\(\Leftrightarrow\left|cosx\right|\left(1-\left|cosx\right|\right)\ge0\) (1)
Do \(0\le\left|cosx\right|\le1\Rightarrow1-\left|cosx\right|\ge0\) với mọi x
\(\Rightarrow\left(1\right)\) luôn đúng với mọi x (đpcm)
PT
1
CM
3 tháng 8 2018
Xét hàm số y = g(x) = tanx - x -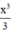 
trên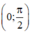 
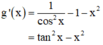
Theo kết quả câu a): tanx > x ∀ x ∈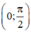 
⇒ g'(x) > 0 ∀ x ∈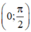 
⇒ y = g'(x) đồng biến trên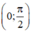 
⇒ g(x) > g(0) = 0 với ∀ x ∈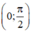 
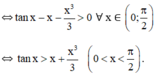
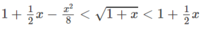
Xét hàm số \(f\left(x\right)=e^x-1-x\) với \(x\ge0\)
Ta có : \(f'\left(x\right)=e^x-1\ge0\) với mọi \(x\ge0\)
và : \(f'\left(x\right)=0\Leftrightarrow x=0\)
\(\Rightarrow f\left(x\right)\) đồng biến với \(x\ge0\) nên với \(x\ge0\Leftrightarrow f\left(x\right)\ge f\left(0\right)=0\)
hay \(e^x-1-x\ge0\) với mọi \(x\ge0\)