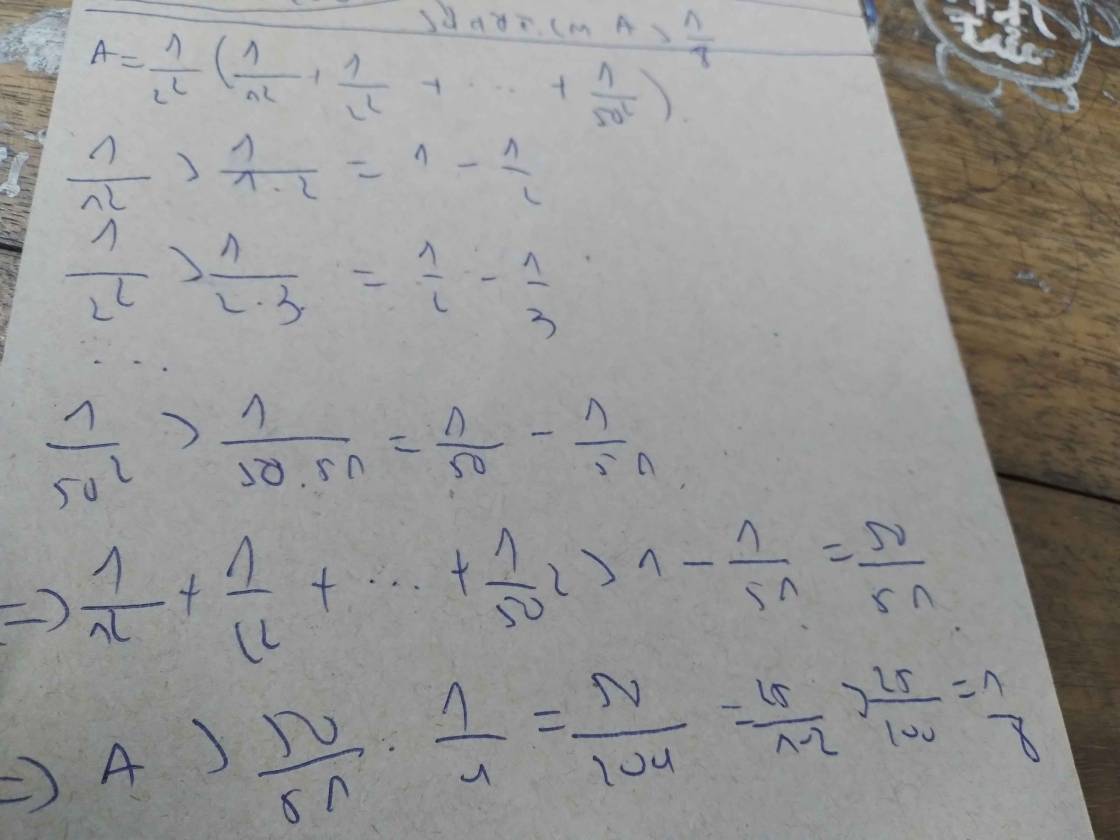Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
chứng minh rằng 1 phần 2 mũ 2 cộng 1 phần 3 mũ 2 + 1 4 mũ 2 chấm chấm chấm 1 phần 100 mũ 2 nhỏ hơn 1


Ta có : \(\frac{1}{2^2}<\frac{1}{1.2}\)
\(\frac{1}{2^3}<\frac{1}{2.3}\)
\(\frac{1}{2^4}<\frac{1}{3.4}\)
..........
\(\frac{1}{2^n}<\frac{1}{\left(n-1\right).n}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+....+\frac{1}{2^n}<\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{\left(n-1\right)n}=1-\frac{1}{n}\)
Mà \(1-\frac{1}{n}<1\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+.....+\frac{1}{2^n}<1\left(đpcm\right)\)

Đặt A=\(\frac{1}{3}.5+\frac{1}{5}.7+...+\frac{1}{97}.99\)
=>A=\(\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{97.99}\)
=>2A=\(\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{97.99}\)
=>2A=\(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}\)
=>2A=\(\frac{1}{3}-\frac{1}{99}=\frac{33}{99}-\frac{1}{99}=\frac{32}{99}\)
=>A=\(\frac{32}{99}:2=\frac{32}{99}.\frac{1}{2}=\frac{32}{198}=\frac{16}{99}\)

Đặt A =\(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\)
Ta có \(3A=3+1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2004}}\)
\(A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\)
=> \(2A=3A-A=3-\frac{1}{3^{2005}}\)
=> \(A-\frac{3-\frac{1}{3^{2005}}}{2}\)

Bạn muốn tính toán giá trị của E hay muốn so sánh E với một số khác?

Đặt A= \(\frac{1}{2}\)-\(\frac{1}{2^2}\)+\(\frac{1}{2^3}\)-\(\frac{1}{2^2}\)+....+\(\frac{1}{2^2}\)
=> 2A=1-\(\frac{1}{2}\)+\(\frac{1}{2^2}\)-\(\frac{1}{23}\)+...+\(\frac{1}{2^{98}}\)
=> 2A+A=1+\(\frac{1}{2^{99}}\)
=> 3A=1+\(\frac{1}{2^{99}}\)
=> A= \(\frac{1}{3}\)+\(\frac{1}{3.2^{99}}\)