Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔACB nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C

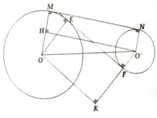
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

a: Xét (O) có
EC,EM là tiếp tuyến
nên EC=EM
mà OM=OC
nên OE là trung trực của CM
=>OE vuông góc với CM
b: Xét (O) có
ΔMCD nội tiếp
CD là đường kính
Do đó: ΔMCD vuôg tại M
=>MD//OE
=>góc MDC=góc EOM