Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
Đáp án B.
Số phần tử của E là 
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là 
. Mỗi bộ 3 chữ số này ta lập được 
số thuộc tập hợp E. Vậy trong tập hợp E có 
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì 
.
Vậy xác suất cần tính là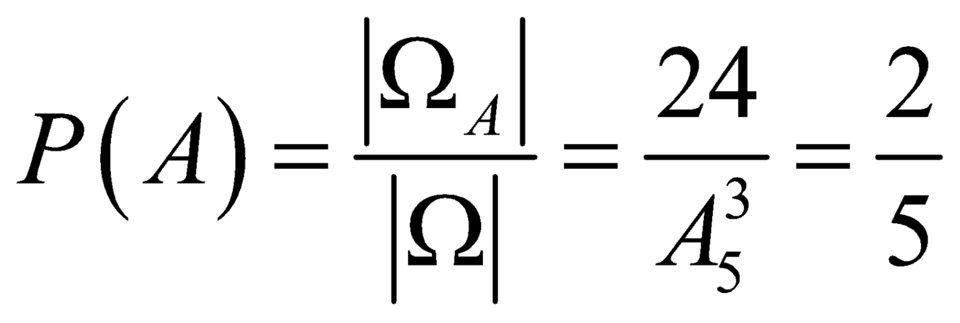 
.
Gọi a b c d ¯ là số có bốn chữ số đôi một khác nhau và thỏa yêu cầu bài toán.
Số các số tự nhiên có bốn chữ số đôi một khác nhau là:
* có 9 cách chọn a.
* Sau khi chọn a, còn 9 số khác a nên có A 9 3 = 504 cách chọn b c d ¯
Suy ra Ω = 9.504 = 4536 .
Đáp án C
Số các số có `8` chữ số đôi một khác nhau là `9.A_9^7`(số)
`=> n(A) = n(\Omega) = 9.A_9^7`
Dễ thấy rằng `0 + 1 + 2 + .. + 9 = 45 \vdots 9`
Gọi `X = {0;1;..;9}`
Để số đó chia hết cho `8` thì nó phải được chọn từ các tập
`X \\ {0;9}` , `X \\ {1;8}` , `X \\ {2;7}` , `X \\ {3;6}` , `X \\ {4;5}`
Ta xét `2` trường hợp như sau:
Trường hợp `1`: Số đó được chọn từ tập `X \\ {0;9}`
Xếp `8` số vào `8` vị trí có `8!`(cách)
Trường hợp `2`:Số đó được chọn từ `4` tập còn lại
Chọn `1` trong `4` tập có `C_4^1`(cách)
Xếp `8` chữ số vừa chọn `1` cách ngẫu nhiên có `8!`(cách)
Cho số `0` đứng đầu xếp `7` số còn lại có `7!` cách
Số lập được:`4(8!-7!)`(số)
Gọi `B` là biến cố chọn được số chia hết cho `9` từ tập `A`
`=> |B| = 8! + 4(8!-7!)`
Xác xuất biến cố `B`:
`P(B) = \frac{8!+4(8!-7!)}{9.A_9^7} = \frac{1}{9}`
Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n( Ω ) = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó A ¯ là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n ∈ ℕ )
* Ta có 
suy ra 
Do đó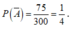 
Đáp án D
Có n ( Ω ) = 9 . 9 . 8 . 7 = 4536 ;
Gọi số đó là a b c d . Số đó muốn chia hết cho 25 thì điều kiện là cd chia hết cho 25. Từ đó c d ∈ { 25 ; 52 ; 50 ; 05 ; 75 ; 57 } .
TH1: c d ∈ { 25 ; 75 } : cd có 4 cách chọn, a:7 cách; b:7 cách => Có 2.7.7 =98 số.
TH2: c d ∈ { 50 } : cd có 2 cách chọn, a:8 cách chọn, b:7 cách => Có 8.7 = 56 số.
Vậy n(A) = 98 + 56 = 154
⇒ p ( A ) = n ( A ) n ( Ω ) = 154 4536 = 11 342 .
.
Đáp án C
Số số tự nhiên gồm 4 chữ số đôi một khác nhau là 
. Không gian mẫu 
có số phần tử là 
.
Gọi A là biến cố “Số được chọn chia hết cho 25”. Gọi số đó có dạng Chọn thì 
.
* Số đó có dạng 
: Chọn a có 7 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
* Số đó có dạng 
: Chọn a có 8 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
* Số đó có dạng 
: Chọn a có 7 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
Vậy số phần tử của biến cố A là
.
Vậy xác suất cần tính là
.
Gọi a b c d ¯ là số có bốn chữ số đôi một khác nhau và thỏa yêu cầu bài toán.
*TH1: nếu d = 5
Có 8 cách chọn a (a khác 0 và a khác d).
Với mỗi cách chọn a có, A 8 2 cách chọn b c ¯
Có 8 . A 8 2 = 448 (số thỏa mãn).
*TH2: Nếu d= 0, có A 9 3 = 504 cách chọn a b c ¯
Nên có 504 số có 4 chữ số khác nhau chia hết cho 5 có chữ số hàng đơn vị là 0.
Vậy số có 4 chữ số khác nhau và chia hết cho 5 là: Ω A = 448 + 504 = 952 .
Đáp án D