Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) =C105=252
c.Gọi C là biến cố:” trong 5 sản phẩm được chọn có đúng một phế phẩm”
n(c)= C21. C84=140 → P( C) =140/252=5/9
Chọn B

Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) =C105=252
a. Gọi A là biến cố:” trong 5 sản phẩm được chọn không có phế phẩm nào”
n(A)= C85=56 → P(A)= 56/252=2/9
Chọn C

Lời giải:
Lấy lần 1 và lần 2 đã lấy ra được 1 sản phẩm loại I và 1 sản phẩm loại II, do đó còn $15$ sản phẩm loại I và $3$ sản phẩm loại II (tổng 18 sản phẩm)
Trong lần thứ 3:
Lấy ngẫu nhiên 1 sản phẩm, có $C^1_18=18$ cách chọn
Lấy ngẫu nhiên 1 sản phẩm loại II từ 3 sản phẩm loại II, có $C^1_3=3$ cách chọn
Xác suất để lấy được sản phẩm loại II: $\frac{3}{18}=\frac{1}{6}$

Đáp án C
Phương pháp giải:
Chia trường hợp của biến cố, áp dụng các quy tắc đếm cơ bản tìm số phần tử của biến cố
Lời giải:
Lấy 6 sản phẩm từ 20 sản phẩm lô hàng có C 20 6 = 38760 cách ⇒ n ( Ω ) = 38760
Gọi X là biến cố 6 sản phẩm lấy ra có không quá 1 phế phẩm. Khi đó, ta xét các trường hợp sau:
TH1. 6 sản phẩm lấy ra 0 có phế phẩm nào => có C 16 6 = 8008 cách
TH2. 6 sản phẩm lấy ra có duy nhất 1 phế phẩm => có C 16 5 . C 4 1 = 17472 cách
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 8008 + 17472 = 25480
Vậy xác suất cần tính là
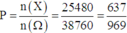
Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là n(Ω) =C105=252
b. Gọi B là biến cố:” trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm” thì :
Chọn C