Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Con lắc lò xo gồm một vật nhỏ có khối lượng m gắn vào đầu một lò xo có độ cứng k và khối lượng không đáng kể.
Từ \(\Delta\)\(l_{0}.k\)\(=mg\)
\(T=2\)\(\pi\)\(\sqrt{\dfrac{m}{k}}\)\(=\dfrac{t}{N}(s)\)
\(f=\dfrac{1}{2π} \)\(\sqrt{\dfrac{k}{m}}\)\(=\dfrac{N}{t}(Hz)\)
\(\omega\)\(=\sqrt{\dfrac{k}{m}}=\)\(\dfrac{2π}{T}=2πf\)
2.
- Động năng của con lắc lò xo:
- Thế năng đàn hồi của con lắc lò:
- Trong con lắc lò xo nằm ngang x = ∆l nên:
- Cơ năng trong con lắc lò xo:
3.Ta có \(F=kx=1,92N\)
\(\omega\)=\(4\)\(\pi\) ;\(m=0,2(kg)\)
\(\Rightarrow\)\(k=m.\)\(\omega\).\(\omega\)=\(32(N/m)\)
\(\Rightarrow\)\(x=0,06\)
\(W_{t}=\dfrac{1}{2}.k.x^{2}=0,0576(J)\)
1.Con lắc lò xo là một hệ thống bao gồm 1 lò xo có độ cứng là k, tạm thời bỏ qua ảnh hưởng của khối lượng (điều kiện lý tưởng): một đầu cố định, một đầu gắn vật nặng có khối lượng m (bỏ qua sự ảnh hưởng của kích thước).
CT tính tần số góc:\(\omega=\sqrt{\dfrac{k}{m}}\)
CT tính chu kì:\(T=2\pi\sqrt{\dfrac{m}{k}}\)
CT tính tần số:\(f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\)
2.Biểu thức tính:
+ Động năng:\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}mA^2sin^2\left(\omega t+\varphi\right)\)
+ Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}kA^2cos^2\left(\omega t+\varphi\right)\)
+ Cơ năng: \(W=W_đ+W_t\)

Đáp án A
Chu kì của con lắc lò xo: 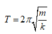
=> T phụ thuộc vào m và k (cấu tạo).

Chọn đáp án B.
Chu kì của con lắc lò xo:
T = 2 π m k
=> T phụ thuộc vào m và k (cấu tạo).

Đáp án C
+ Từ bảng số liệu, ta thấy rằng động năng cực đại của vật E d m a x = E = 6 m J → ban đầu vật đi qua vị trí cân bằng.
Sau khoảng thời gian 0,125T động năng giảm một nửa → t 1 = T 6 − T 8 = T 24
+ Tại thời điểm T 6 sau khoảng thời gian 0,125T tiếp theo vật đến biên (có động năng bằng 0) → t 3 = T 6 + T 8 = 7 T 24 .
Thời điểm t 4 ứng với vị trí thế năng bằng 3 lần động năng x = ± 3 2 A → t 4 = 7 T 24 + T 12 = 3 T 8
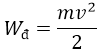
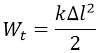
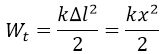
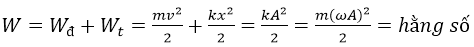
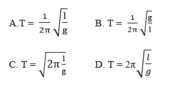
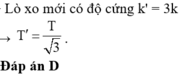
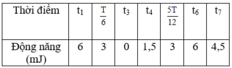
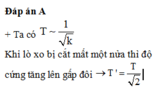
Chọn đáp án D.