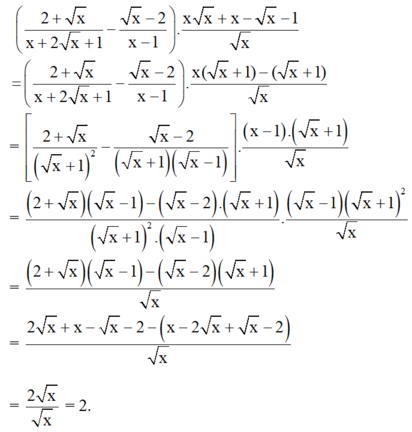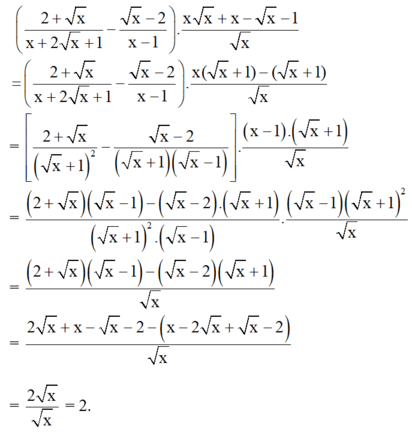Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với x > 0; x ≠ 4; x ≠ 9 ta có:
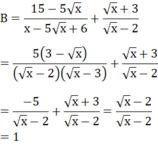
Vậy giá trị của B không phụ thuộc vào giá trị của biến x

\(\frac{2x}{x+3\sqrt{x}+2}+\frac{5\sqrt{x}+1}{x+4\sqrt{x}+3}+\frac{\sqrt{x}+10}{x+5\sqrt{x}+6}\)
\(=\frac{2x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}+\frac{5\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}+10}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\left(\sqrt{x}+3\right)+\left(5\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+\left(\sqrt{x}+10\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2\sqrt{x^3}+6x+5x+11\sqrt{x}+2+x+11\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{12x+22\sqrt{x}+2\sqrt{x^3}+12}{6x+11\sqrt{x}+\sqrt{x^3}+6}\)
\(=\frac{2\left(6x+11\sqrt{x}+\sqrt{x^3}+6\right)}{6x+11\sqrt{x}+\sqrt{x^3}+6}\)
\(=2\) (ko phụ thuộc vào biến ) (đpcm)

\(x^2-\left(2a-1\right)x-4a-3=0\)
\(\Delta=\left(2a-1\right)^2+4\left(4a+3\right)\)
\(=4a^2-4a+1+16a+12\)
\(=4a^2+12a+13=\left(2a+3\right)^2+4>0\)
Vì \(\Delta>0\Rightarrow\) phương trình có 2 nghiệm phân biệt với mọi a
Vì phương trình có 2 nghiệm phân biệt, áp dụng hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2a-1\\x_1.x_2=-4a-3\end{matrix}\right.\) ⇒ \(x_1.x_2+2\left(x_1+x_2\right)=-5\)
Ta có:
\(A=x_1^2+x^2_2=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=\left(2a-1\right)^2-2\left(-4a-3\right)\)
\(=4a^2-4a+1+8a+6\)
\(=\left(2a+1\right)^2+6\)
Vì \(\left(2a+1\right)^2\ge0\forall a\)
⇒\(A\ge6\)
Min A=6 <=> \(a=-\dfrac{1}{2}\)

Hướng dẫn trả lời:
ĐKXĐ: 0 < x ≠ 1.
Đặt √x = a (a > 0 và a ≠ 1)
Ta có:
(2+√xx+2√x+1−√x−2x−1).x√x+x−√x−1√x=[2+aa2+2a+1−a−2a2−1].a3+a2−a−1a=[(2+a)(a−1)−(a−2)(a+1)(a+1)(a2−1)].(a+1)(a2−1)a=2a(a+1)(a2−1).(a+1)(a2−1)a=2

\(R=\frac{2x}{x+3\sqrt{x}+2}+\frac{5\sqrt{x}}{x+4\sqrt{x}+3}+\frac{\sqrt{x}+10}{x+5\sqrt{x}+6}\)
\(=\frac{2x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}+\frac{5\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}+10}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
=\(\frac{2x\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}+\frac{5\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}+\frac{\left(\sqrt{x}+10\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+6x+5x+10\sqrt{x}+x+\sqrt{x}+10\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+12x+21\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
@@@@@@@@@@@ Đề sai hay mình sai??@@@@@@@@@@