Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có x-y-z=0
->x=y+z
y=x-z
z=x-y
B=\(\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1-\dfrac{y}{z}\right)\)
B=\(\left(\dfrac{x-z}{x}\right)\left(\dfrac{y-x}{y}\right)\left(\dfrac{z+y}{z}\right)\)
B=\(\dfrac{y}{x}.\left(-\dfrac{z}{y}\right)\left(\dfrac{x}{z}\right)\)
B=\(\dfrac{-\left(xyz\right)}{xyz}\)
B=-1

Vào đây:
Câu hỏi của Phạm Đức Minh - Toán lớp 7 | Học trực tuyến

\(\dfrac{y+z-x}{x}=\dfrac{z+x-y}{y}=\dfrac{x+y-z}{z}\)
\(\Rightarrow\dfrac{y+z-x}{x}+2=\dfrac{z+x-y}{y}+2=\dfrac{x+y-z}{z}+2\)
\(\Rightarrow\dfrac{x+y+z}{x}=\dfrac{x+y+z}{y}=\dfrac{x+y+z}{z}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x+y+z}{x}=\dfrac{x+y+z}{y}\\\dfrac{x+y+z}{y}=\dfrac{x+y+z}{z}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\left(x+y+z\right)=y\left(x+y+z\right)\\y\left(x+y+z\right)=z\left(x+y+z\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(x+y+z\right)=0\\\left(y-z\right)\left(x+y+z\right)=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=y\\x+y+z=0\end{matrix}\right.\\\left[{}\begin{matrix}y=z\\x+y+z=0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=y=z\\x+y+z=0\end{matrix}\right.\)
\(\circledast\) Với \(x=y=z\) thì \(A=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)=\left(1+1\right)\left(1+1\right)\left(1+1\right)=8\)
\(\circledast\) Với \(x+y+z=0\) thì\(\left\{{}\begin{matrix}x+y=-z\\x+z=-y\\y+z=-x\end{matrix}\right.\)
Khi đó \(A=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)=\dfrac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{xyz}=\dfrac{-xyz}{xyz}=-1\)
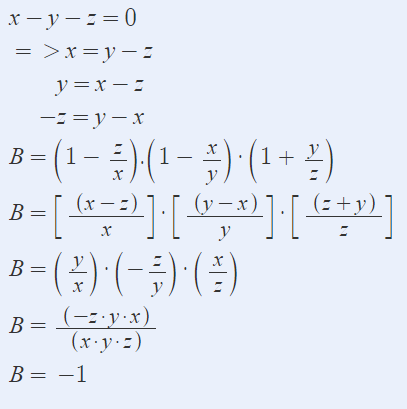
Ta có: x-y-z=0 <=> x=y+z Thay vào A ta có:
A=\(\left(1-\dfrac{z}{y+z}\right)\left(1-\dfrac{y+z}{y}\right)\left(1+\dfrac{y}{z}\right)\)
=\(\dfrac{y}{y+z}\cdot\left(-\dfrac{z}{y}\right)\cdot\dfrac{y+z}{z}=\dfrac{y}{z}\cdot\left(-\dfrac{z}{y}\right)=-1\)
Vậy A=-1
theo bài ra táo:
\(A=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\\ \Rightarrow A=\dfrac{x-z}{x}.\dfrac{y-x}{y}.\dfrac{z+y}{z}\left(1\right)\)
ta lại có:
\(x-y-z=0\\ \Rightarrow\left\{{}\begin{matrix}x-z=y\left(2\right)\\y-x=-z\left(3\right)\\z+y=x\left(4\right)\end{matrix}\right.\)
thay 2;3;4 vào 1 ta có:
\(A=\dfrac{y}{x}.\dfrac{-z}{y}.\dfrac{x}{z}=-1\)
vậy A = -1