Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T=\dfrac{\left(xy\right)^2}{zx+zy}+\dfrac{\left(yz\right)^2}{xy+xz}+\dfrac{\left(zx\right)^2}{yx+yz}\ge\dfrac{xy+yz+zx}{2}\ge\dfrac{3}{2}\sqrt[3]{\left(xyz\right)^2}=\dfrac{3}{2}\)

\(\dfrac{\sqrt{1+x^3+y^3}}{xy}>=\sqrt{\dfrac{3}{xy}}\)
\(\dfrac{\sqrt{1+y^3+z^3}}{yz}>=\sqrt{\dfrac{3}{yz}}\)
\(\dfrac{\sqrt{1+z^3+x^3}}{xz}>=\sqrt{\dfrac{3}{xz}}\)
=>\(VT>=\sqrt{3}\left(\dfrac{1}{\sqrt{xy}}+\dfrac{1}{\sqrt{yz}}+\dfrac{1}{\sqrt{xz}}\right)=3\sqrt{3}\)

\(P=\dfrac{\sqrt{x}}{\sqrt{xy}+\sqrt{x}+3}+\dfrac{\sqrt{y}}{\sqrt{yz}+\sqrt{y}+1}+\dfrac{3\sqrt{z}}{\sqrt{zx}+3\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}}{\sqrt{xy}+\sqrt{x}+\sqrt{xyz}}+\dfrac{\sqrt{y}}{\sqrt{yz}+\sqrt{y}+1}+\dfrac{\sqrt{xyz}\sqrt{z}}{\sqrt{zx}+\sqrt{xyz}\sqrt{z}+\sqrt{xyz}}\)
\(=\dfrac{1}{\sqrt{y}+1+\sqrt{yz}}+\dfrac{\sqrt{y}}{\sqrt{yz}+\sqrt{y}+1}+\dfrac{\sqrt{yz}}{1+\sqrt{yz}+\sqrt{y}}\)
\(=\dfrac{1+\sqrt{y}+\sqrt{yz}}{1+\sqrt{y}+\sqrt{yz}}=1\)
\(\Rightarrow\sqrt{10P-1}=\sqrt{10.1-1}=\sqrt{9}=3\)

Lời giải:
Từ \(xy+yz+xz=xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
Đặt \((a,b,c)=\left(\frac{1}{x}; \frac{1}{y}; \frac{1}{z}\right)\Rightarrow a+b+c=1\)
BĐT cần chứng minh trở thành:
\(P=\frac{c^3}{(a+1)(b+1)}+\frac{a^3}{(b+1)(c+1)}+\frac{b^3}{(c+1)(a+1)}\geq \frac{1}{16}(*)\)
Thật vậy, áp dụng BĐT Cauchy ta có:
\(\frac{c^3}{(a+1)(b+1)}+\frac{a+1}{64}+\frac{b+1}{64}\geq 3\sqrt[3]{\frac{c^3}{64^2}}=\frac{3c}{16}\)
\(\frac{a^3}{(b+1)(c+1)}+\frac{b+1}{64}+\frac{c+1}{64}\geq 3\sqrt[3]{\frac{a^3}{64^2}}=\frac{3a}{16}\)
\(\frac{b^3}{(c+1)(a+1)}+\frac{c+1}{64}+\frac{a+1}{64}\geq 3\sqrt[3]{\frac{b^3}{64^2}}=\frac{3b}{16}\)
Cộng theo vế các BĐT trên và rút gọn :
\(\Rightarrow P+\frac{a+b+c+3}{32}\geq \frac{3(a+b+c)}{16}\)
\(\Leftrightarrow P+\frac{4}{32}\geq \frac{3}{16}\Leftrightarrow P\geq \frac{1}{16}\)
Vậy \((*)\) được chứng minh. Bài toán hoàn tất.
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{3}\Leftrightarrow x=y=z=3\)
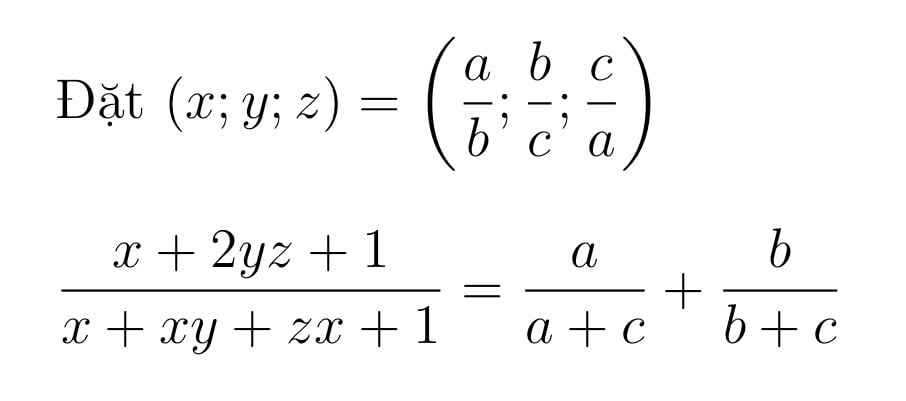
Dòng cuối sao ra tử như v bạn