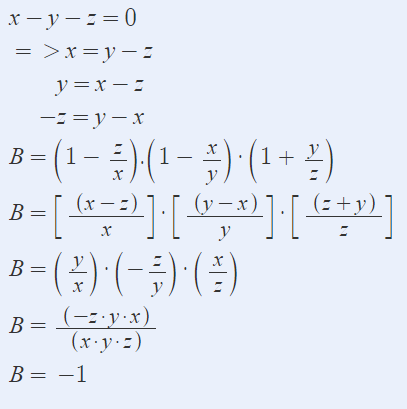K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DC
1
AH
Akai Haruma
Giáo viên
29 tháng 3 2021
Lời giải:
$A=\frac{(x+z)(z-y)(y-z)}{yz^2}=\frac{-(x+z)(y-z)^2}{yz^2}$
Vì $-x+y-z=0$ nên $-(x+z)=-y$
$y-z=x$
$\Rightarrow A=\frac{-yx^2}{yz^2}=\frac{-x^2}{z^2}$
Đến đây là kịch rồi bạn ạ, không tính được giá trị cụ thể của biểu thức A. Bạn xem lại đề.
28 tháng 3 2017
x-y-z=0
\(\Rightarrow x=y+z\)
\(\Rightarrow y=x-z\)
\(\Rightarrow-z=y-z\)
\(B=\left(1-\dfrac{z}{x}\right).\left(1-\dfrac{y}{x}\right).\left(1+\dfrac{y}{z}\right)\)
\(B=\left(\dfrac{x-z}{x}\right).\left(\dfrac{y-x}{y}\right).\left(\dfrac{z+y}{z}\right)\)
\(B=(\dfrac{y}{x}).\left(\dfrac{-z}{y}\right).\left(\dfrac{x}{z}\right)\)
\(B=\dfrac{\left(y.x.-z\right)}{\left(y.x.z\right)}\Rightarrow B=-1\)
