
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Phương pháp:
Tìm TXĐ của hàm số, sau đó tìm GTLN, GTNN của hàm số sau đó chọn đáp án đúng.
Cách giải:
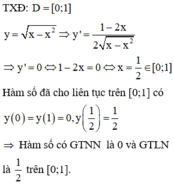

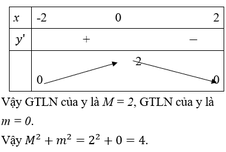
Đáp án D
Phương pháp: Sử dụng phương pháp hàm số, tìm GTLN, GTNN của y = f(x) trên [a;b]
Bước 1: Tính f’(x) giải phương trình f’(x) = 0, tìm các nghiệm ![]()
Bước 2: Tính các giá trị ![]()
Bước 3: So sánh và kết luận
![]()
![]()
Cách giải:
y = x 4 - x 2
![]()
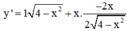
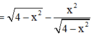

![]()
![]()
![]()
![]()
![]()
![]()
![]()

Chọn C.
f'(x) = 2xex + ex(x2 – 3) = 0 ![]()
Ta có f(0) = -3
f(1) = -2e = m
f(2) = e2 = M
Suy ra (m2 – 4M)2016 = 0

Chọn đáp án B
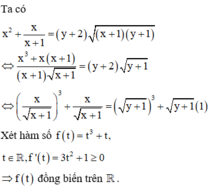
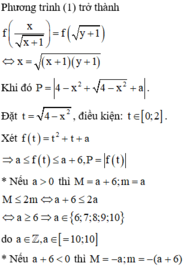
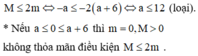
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
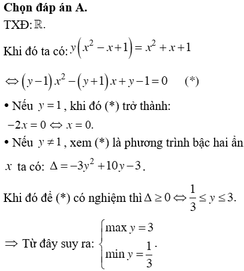
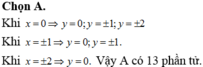
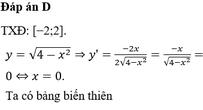
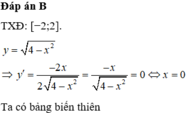

\(A=\frac{1}{2}\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\frac{1}{2}\left(x+y\right)^2=\frac{1}{2}\)
Min A= 1/2 khi x = y =1/2
Vì x+y=1
=>y=1-x
Ta có: \(A=x^2+y^2=x^2+\left(1-x\right)^2=x^2+1\left(1-x\right)-x\left(1-x\right)=x^2+1-x-x+x^2\)
\(A=2x^2-2x+1=2.\left(x^2-x+\frac{1}{2}\right)\)
\(A=2.\left(x^2-\frac{1}{2}x-\frac{1}{2}x+\frac{1}{4}-\frac{1}{4}+\frac{1}{2}\right)=2\left[x\left(x-\frac{1}{2}\right)-\frac{1}{2}\left(x-\frac{1}{2}\right)+\frac{1}{4}\right]\)
\(A=2\left[\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\right]=2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}\)
Vì \(2\left(x-\frac{1}{2}\right)^2>=0\) với mọi x
=>\(2\left(x-\frac{1}{2}\right)^2+\frac{1}{2}>=\frac{1}{2}\) với mọi x
Dấu "=" xảy ra <=>\(x=\frac{1}{2}\);mà x+y=1=>\(y=\frac{1}{2}\)
Khi đó GTNN của A=x2+y2 là 1/2 tại \(x=y=\frac{1}{2}\)