Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : x3+y3+z3=3xyz
<=>x3+y3+3x2y+3xy2+z3-3xyz-3x2y-3xy2=0
<=>(x+y)3+z3-3xy.(x+y+z)=0
<=>(x+y+z)[(x+y)2-(x+y).z+z2]-3xy.(x+y+z)=0
<=>(x+y+z).(x2+2xy+y2-xz-yz+z2-3xy)=0
<=>(x+y+z)(x2+y2+z2-xy-yz-xz)=0
<=>x+y+z=0(loại) hoặc x2+y2+z2-xy-yz-xz=0
*x2+y2+z2-xy-yz-xz=0
<=>2x2+2y2+2z2-2xy-2yz-2xz=0
<=>(x-y)2+(y-z)2+(z-x)2=0
<=>x=y=z
Suy ra: \(P=\frac{xyz}{\left(x+x\right)\left(y+y\right)\left(z+z\right)}=\frac{xyz}{2x.2y.2z}=\frac{1}{8}\)

\(2P=2x^2-2y^2-2xy-2x+2y+2\)
\(2P=\left(x-y\right)^2+\left(1-x\right)^2+\left(y+1\right)^2\)
Áp dụng BĐT Bunhiacopxki:
\(\left(1^2+1^2+1^2\right)\left[\left(x-y\right)^2+\left(1-x\right)^2+\left(y+1\right)^2\right]\ge\left(x-y+1-x+y+1\right)^2\)
\(3.2M\ge4\)
\(\Leftrightarrow M\ge\dfrac{2}{3}\)
Mmin\(=\dfrac{2}{3}\Leftrightarrow\dfrac{1}{x-y}=\dfrac{1}{1-x}=\dfrac{1}{y+1}\)
\(\Leftrightarrow x=\dfrac{1}{3};y=\dfrac{-1}{3}\)

Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .
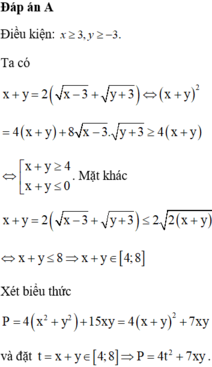
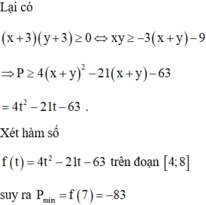

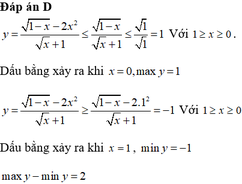
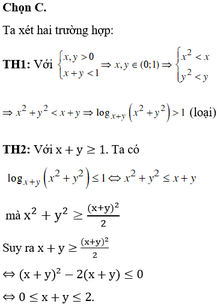
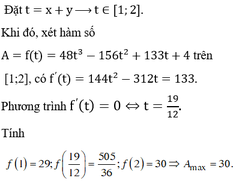
Đáp án C
log 3 2 x + y + 1 x + y = x + 2 y ⇔ log 3 2 x + y + 1 − log 3 x + y = 3 x + y − 2 x + y + 1 + 1 ⇔ log 3 2 x + y + 1 + 2 x + y + 1 = log 3 3 x + y + 3 x + y *
Xét hàm số f t = log 3 t + t trên khoảng 0 ; + ∞ ⇒ f t là hàm số đồng biến trên 0 ; + ∞
Mà * ⇔ f 2 x + y + 1 = f 3 x + 3 y ⇔ 2 x + y + 1 = 3 x + 3 y ⇔ x + 2 y = 1
Đặt a = y > 0 ⇔ y = a 2 ⇔ x = 1 − 2 y = 1 − 2 a 2 , khi đó T = g a = 1 1 − 2 a 2 + 2 a
Xét hàm số g a = 1 1 − 2 a 2 + 2 a trên khoảng 0 ; 1 2 , suy ra min 0 ; 1 2 g a = 6
Vậy giá trị nhỏ nhất cần tìm là T min = 6