
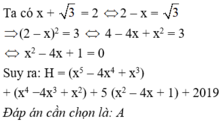
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

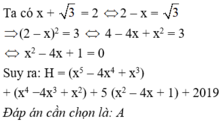

\(\Leftrightarrow x=2-\sqrt{3}\)
Dễ thấy x là nghiệm của PT \(x^2-4x+1\)
\(H=\left(x^5-4x^4+x^3\right)+\left(x^4-4x^3+x^2\right)+\left(5x^2-20x+5\right)+2019\\ H=\left(x^2-4x+1\right)\left(x^3+x^2+5\right)+2019\\ H=2019\)

Đề lỗi font. Bạn cần chỉnh sửa lại bằng công thức toán để được hỗ trợ tốt hơn.

Để H lớn nhất thì \(\frac{1}{H}=\frac{\left(x+2018\right)^2}{x}\) nhỏ nhất.
Ta có: \(\frac{1}{H}=\frac{x^2+2.x.2018+2018^2}{x}=x+4036+\frac{2018^2}{x}\)
\(\frac{x+\frac{2018^2}{x}}{2}\ge\sqrt{x.\frac{2018^2}{x}}=2018\) (áp dụng bất đẳng thức cosi) \(\Rightarrow x+\frac{2018^2}{x}\ge4036\)
\(\frac{1}{A}\ge4036+4036=8072\Rightarrow A\le\frac{1}{8072}\)
Dấu "=" xảy ra khi: \(x=\frac{2018^2}{x}\Rightarrow x^2=2018^2\Rightarrow x=2018\left(x>0\right)\)
Vậy GTLN của H là \(\frac{1}{8072}\Leftrightarrow x=2018\)

Giải:
Ta có:
\(\left(\sqrt{2018}+\sqrt{2020}\right)^2\)
\(=2018+2020+2\sqrt{2018.2020}\)
\(=2019+2019+2\sqrt{\left(2019-1\right)\left(2019+1\right)}\)
\(=2.2019+2\sqrt{\left(2019-1\right)\left(2019+1\right)}\)
\(=2.2019+2\sqrt{2019^2-1^2}< 2.2019+2.2019\)
\(\Leftrightarrow2.2019+2\sqrt{2019^2-1^2}< 4.2019\)
\(\Leftrightarrow2.2019+2\sqrt{2019^2-1^2}< \left(2\sqrt{2019}\right)^2\)
\(\Leftrightarrow\sqrt{2018}+\sqrt{2020}< 2\sqrt{2019}\)
Vậy ...

a + b + c = 6
=> (a + b + c)2 = 36
<=> a2 + b2 + c2 + 2(ab + bc + ca) = 36
<=> a2 + b2 + c2 = 36 - 2.12 = 12
<=> a2 + b2 + c2 = ab + bc + ca
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
<=> a = b = c
=> a = b = c = 2
P = (a - 3)2018 + (b - 3)2018 + (c - 3)2018 = (-1)2018 + (-1)2018 + (-1)2018 = 1 + 1 + 1 = 3

Bài làm:
Ta có:
\(D=\frac{1}{\sqrt{h+2\sqrt{h-1}}}+\frac{1}{\sqrt{h-2\sqrt{h-1}}}\)
\(D=\frac{1}{\sqrt{\left(h-1\right)+2\sqrt{h-1}+1}}+\frac{1}{\sqrt{\left(h-1\right)-2\sqrt{h-1}+1}}\)
\(D=\frac{1}{\sqrt{\left(\sqrt{h-1}+1\right)^2}}+\frac{1}{\sqrt{\left(\sqrt{h-1}-1\right)^2}}\)
\(D=\frac{1}{\left|\sqrt{h-1}+1\right|}+\frac{1}{\left|\sqrt{h-1}-1\right|}\)
Tại h = 3 thì giá trị của D là:
\(D=\frac{1}{\left|\sqrt{3-1}+1\right|}+\frac{1}{\left|\sqrt{3-1}-1\right|}\)
\(D=\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{2}-1}=\frac{\sqrt{2}-1+\sqrt{2}+1}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}=\frac{2\sqrt{2}}{2-1}=2\sqrt{2}\)