ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
21 tháng 10 2017

Cho x > 0; y > 0. Tìm khẳng định đúng trong các khẳng định sau?

A. (1)

B. (2)

C. (3)

D. (1); (2)
#Toán lớp 8
1
CM
Cao Minh Tâm
21 tháng 10 2017

Đúng(0)
PT
Pham Trong Bach
21 tháng 2 2018
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình x 2 + 3 x x = 0  là {0; 3}b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0  là {-2}c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8  là {0} A. 1                       B. 2  ...
Đọc tiếp

Trong các khẳng định sau, số khẳng định đúng là:

a) Tập nghiệm của phương trình x 2 + 3 x x = 0  là {0; 3}

b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0  là {-2}

c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8  là {0}

A. 1                      

B. 2                      

C. 0                      

D. 3
#Toán lớp 8
1
CM
Cao Minh Tâm
21 tháng 2 2018

Đáp án cần chọn: A

Đúng(0)
PT
Pham Trong Bach
1 tháng 11 2018
Hãy xét xem các khẳng định sau đúng hay sai? Vì sao?a) − 3 . ( 2 ) > 6                 b) 2 − 1 5 < − 1 5 + 2  c) − 2 + 3 < 7 ;              d) − x 2 − 1 ≤ 0 ...
Đọc tiếp

Hãy xét xem các khẳng định sau đúng hay sai? Vì sao?

a) − 3 . ( 2 ) > 6                 b) 2 − 1 5 < − 1 5 + 2  

c) − 2 + 3 < 7 ;              d) − x 2 − 1 ≤ 0

#Toán lớp 8
1
CM
Cao Minh Tâm
1 tháng 11 2018

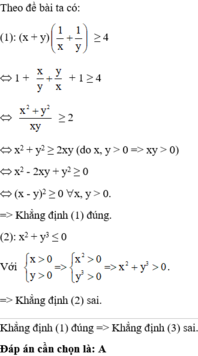
a) Khẳng định sai;         b) Khẳng định sai;

c) Khẳng định đúng;      d) Khẳng định đúng.

Đúng(0)
PT
Pham Trong Bach
14 tháng 6 2017
Cho các khẳng định sau:(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4Số khẳng định đúng là: A. 0 B. 1 C. 2 D....
Đọc tiếp

Cho các khẳng định sau:

(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2

(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt

(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4

Số khẳng định đúng là:

A. 0

B. 1

C. 2

D. 3
#Toán lớp 8
1
CM
Cao Minh Tâm
14 tháng 6 2017

Xét phương trình |x – 3| = 1

TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3

Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)

TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3

Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)

Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng

|x – 1| = 0 ó x – 1 = 0  ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.

Vậy có 1 khẳng định đúng

Đáp án cần chọn là: B

Đúng(0)
T
Tuyền
22 tháng 11 2021

Trong các khẳng định sau, khẳng định nào đúng:

A. ( 2x - 1 )2 = ( 1 - 2x) 2

B. x 2 - 1 = 1 - x 2

C. ( x - 1 ) 3 = ( 1 - x ) 3 

D. Cả 3 câu đều đúng
#Toán lớp 8
5
I
ILoveMath
22 tháng 11 2021

A

Đúng(0)
H
๖ۣۜHả๖ۣۜI
22 tháng 11 2021

A

Đúng(0)
PT
Pham Trong Bach
11 tháng 4 2017
Các khẳng định sau đây đúng hay sai:a. Phương trình  4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.b. Phương trình  x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0  có tập nghiệm S = {-2; 1}c. Phương trình  x 2 + 2 x + ...
Đọc tiếp

Các khẳng định sau đây đúng hay sai:

a. Phương trình  4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.

b. Phương trình  x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0  có tập nghiệm S = {-2; 1}

c. Phương trình  x 2 + 2 x + 1 x + 1 = 0  có nghiệm x = - 1

d. Phương trình  x 2 x - 3 x = 0  có tập nghiệm S = {0; 3}
#Toán lớp 8
1
CM
Cao Minh Tâm
11 tháng 4 2017

a. Đúng

Vì x 2  + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:

4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2

b. Đúng

Vì  x 2  – x + 1 = x - 1 / 2 2  + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:

(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0

⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1

c. Sai

Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1

Do vậy phương trình Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 không thể có nghiệm x = - 1

d. Sai

Vì điều kiện xác định của phương trình là x ≠ 0

Do vậy x = 0 không phải là nghiệm của phương trình Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Đúng(0)
PT
Pham Trong Bach
10 tháng 6 2019
Cho biết a < b. Trong các khẳng định sau, số khẳng định đúng là?(I) a - 1 < b - 1         (II) a - 1 < b        (III) a + 2 < b + 1 A. 1 B. 2 C. 3 D....
Đọc tiếp

Cho biết a < b. Trong các khẳng định sau, số khẳng định đúng là?

(I) a - 1 < b - 1         (II) a - 1 < b        (III) a + 2 < b + 1

A. 1

B. 2

C. 3

D. 0
#Toán lớp 8
1
CM
Cao Minh Tâm
10 tháng 6 2019

+ Vì a < b, cộng hai vế của bất đẳng thức với -1 ta được: a - 1 < b - 1 => (I) đúng.

+ Vì a - 1 < b - 1 (cmt) mà b - 1 < b nên a - 1 < b => (II) đúng.

+ Vì a < b, cộng hai vế của bất đẳng thức với 1 ta được: a + 1 < b + 1 mà

a + 1 < a + 2 nên ta chưa đủ dữ kiện để nói rằng a + 2 < b + 1 => (III) sai.

Do đó có 2 khẳng định đúng.

Đáp án cần chọn là: B

Đúng(0)
PT
Pham Trong Bach
11 tháng 1 2017

Trong các khẳng định sau đây, khẳng định nào sai?

( 1 )    ( - 4 ).5 < ( - 5 ).4

( 2 )    ( - 7 ).12 ≥ ( - 7 ).11

( 3 )     - 4 x 2 > 0

A. ( 1 ),( 2 ) và ( 3 )   

B. ( 1 ),( 2 ) 

C. ( 1 )   

D. ( 2 ),( 3 ) 
#Toán lớp 8
1
CM
Cao Minh Tâm
11 tháng 1 2017

+ Ta có: ( - 4 ).5 = 4.( - 5 ) → Khẳng định ( 1 ) sai.

+ Ta có: 12 > 11 ⇒ 12.( - 7 ) < 11.( - 7 ) → Khẳng định ( 2 ) sai.

+ Ta có: x 2 ≥ 0 ⇒ - 4 x 2 ≤ 0  → Khẳng định ( 3 ) sai

Chọn đáp án A.

Đúng(0)
PT
Pham Trong Bach
4 tháng 2 2019

Trong các khẳng định sau đây, khẳng định nào sai?

( 1 )    ( - 4 ).5 ≤ ( - 5 ).4

( 2 )     ( - 7 ).12 ≥ ( - 7 ).11

( 3 )     - 4 x 2 > 0

A. ( 1 ),( 2 ) và ( 3 )   

B. ( 1 ),( 2 ) 

C. ( 1 )   

D. ( 2 ),( 3 ) 
#Toán lớp 8
1
CM
Cao Minh Tâm
4 tháng 2 2019

Ta có:  ( − 4 ) .5 = 4. ( − 5 ) nên khẳng định (1) đúng.

Vì  12 > 11 ⇒ 12. − 7 < 11. − 7  nên khẳng định (2) sai.

Vì  x 2 ≥ 0 ⇒ − 4 x 2 ≤ 0 nên khẳng định (3) sai.

Chọn đáp án D.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP