Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x_1^2+\frac{v_1^2}{\omega^2}=x_2^2+\frac{v_2^2}{\omega^2}\Rightarrow\omega=\sqrt{\frac{v_2^2-v_1^2}{x_1^2-x_2^2}}=10\pi\)
Do pt của 4 ngoại lực có biên độ bằng nhau, để con lắc dao động với biên độ nhỏ nhất trong giai đoạn ổn định thì \(\left|\omega-\omega_F\right|\) là lớn nhất
\(\Rightarrow\) Đáp án B đúng (không chắc lắm :( )

Đáp án D
Phương pháp: Áp dụng điều kiện xảy r hiện tượng cộng hưởng trong đoạn mạch RLC nối tiếp
Cách giải:
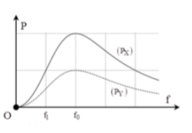
Với uX trễ pha hơn uY ta dễ thấy rằng X chứa RX và ZC, Y chứa RY và ZL.
+ Từ đồ thị, ta thấy rằng, khi f = f0 mạch xảy ra cộng hưởng ZL0 = ZC0 ta chuẩn hóa Z L 0 = Z C 0 = 1
+ Khi 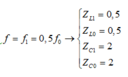 .
.
Mặt khác 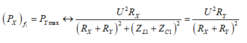
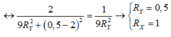
Độ lệch pha giữa u Y và u X :
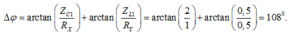

Đáp án D.
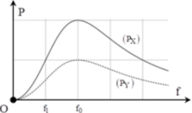
Với Ux trễ pha hơn Uy ta dễ thấy rằng X chứa Rx và Zc, Y chứa Ry và Z L
+ Từ đồ thị, ta thấy rằng, khi f=fo mạch xảy ra cộng hưởng,
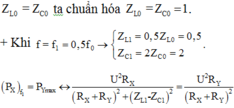
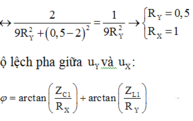
![]()

Đặt F' = F-2, suy ra: F'=-80.x là lực hồi phục (F=-k.x)
Vậy k = 80(N/m)
\(\Rightarrow \omega = \sqrt{\dfrac{k}{m}}= \sqrt{\dfrac{80}{0,2}}=4\pi(rad/s)\)
Tốc độ cực đại: \(v_{max}=\omega A = 4\pi.7,5=30\pi (cm/s)\)

Tần số góc: \(\omega = 2\pi/T = 4\pi (rad/s)\)
Độ cứng lò xo: \(k=m.\omega^2=0,4.(4\pi)^2=64(N/m)\)
Lực đàn hồi cực đại tác dụng vào vật: \(F_{dhmax}=k.A = 64.0,08=5,12N\)
Tan so goc:=2 π/T=4π (rad/s)
Do cung lo xo:k=m.w2=0,4.(4π)2 =64(N/m)
Luc dan hoi cuc dai tac dung vao vat:
Fd/max=K..A=64.0,08=5,12N

Vật kéo xuống 5cm từ VTCB và thả không vận tốc đầu nên A=5cm
\(\Delta l_0=\frac{mg}{k}=0,05\left(m\right)=5\left(cm\right)\)
Nhận thấy \(A=\Delta l_0\) nên:
+) \(F_{min}=0\left(N\right)\)
+) \(F_{max}=k\left(\Delta l_0+A\right)=40\left(0,05+0,05\right)=4\left(N\right)\)
FX = FY = F.cos600 = 12.0,5 = 6 N. Chọn D.