K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 2 2017
công thức tính diện tích của tứ giác có 2 đường chéo vuông góc nhau là: tích 2 đường chéo chia 2
Áp dụng: kết quả là 48cm2
KA
1
NT
0
KA
1
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
a.
Xét hai tam giác MNP và MQP có:
\(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\\MP\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MNP=\Delta MQP\left(c.c.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{NMP}=\widehat{QMP}\\\widehat{NPM}=\widehat{QPM}\end{matrix}\right.\) hay MP là phân giác của góc M và P
b.
Do \(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\end{matrix}\right.\) \(\Rightarrow MP\) là trung trực NQ
\(\Rightarrow MP\perp NQ\) (đpcm)
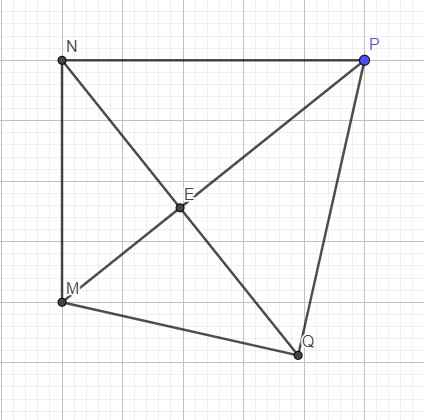
Gọi MP ∩ NQ = {O}
Ta có :
\(S_{MNPQ}=S_{MON}+S_{NOP}+S_{POQ}+S_{QOM}\)
\(\Rightarrow S_{MNPQ}=\frac{1}{2}OM.ON+\frac{1}{2}ON.OP+\frac{1}{2}OP.OQ+\frac{1}{2}OQ.OM\)
\(\Rightarrow S_{MNPQ}=\frac{1}{2}OM\left(ON+OQ\right)+\frac{1}{2}OP\left(ON+OQ\right)\)
\(\Rightarrow S_{MNPQ}=\frac{1}{2}OM.NQ+\frac{1}{2}OP.NQ\)
\(\Rightarrow S_{MNPQ}=\frac{1}{2}NQ\left(OM+OP\right)\)
\(\Rightarrow S_{MNPQ}=\frac{1}{2}NQ.MP\)
\(\Rightarrow S_{MNPQ}=\frac{18.24}{2}=216\left(cm^2\right)\)
Vậy diện tích tứ giác MNPQ là 216 cm2