Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMNP và ΔPQM có
MN=PQ
NP=QM
MP chung
=>ΔMNP=ΔPQM
b: Xét tứ giác MNPQ có
MQ=NP
MN=PQ
=>MNPQ là hình bình hành
=>MN//PQ và MQ//NP

a: Xét ΔMKH có MK=MH
nên ΔMKH cân tại M
b: Xét ΔKMN và ΔHMP có
MK=MH
\(\widehat{KMN}=\widehat{HMP}\)
MN=MP
Do đó: ΔKMN=ΔHMP
c: Ta có: ΔMKH cân tại M
mà MQ là đường trung tuyến
nên MQ là đường cao

a) Xét ΔMFE và ΔPFQ có
MF=PF(F là trung điểm của MP)
\(\widehat{MFE}=\widehat{PFQ}\)(hai góc đối đỉnh)
FE=FQ(F là trung điểm của EQ)
Do đó: ΔMFE=ΔPFQ(c-g-c)
hay ME=PQ(hai cạnh tương ứng)
mà ME=NE(E là trung điểm của MN)
nên NE=PQ(đpcm)
b) Ta có: ΔMFE=ΔPFQ(cmt)
nên \(\widehat{EMF}=\widehat{QPF}\)(hai góc tương ứng)
mà \(\widehat{EMF}\) và \(\widehat{QPF}\) là hai góc ở vị trí so le trong
nên ME//PQ(Dấu hiệu nhận biết hai đường thẳng song song)
hay NE//PQ
⇒\(\widehat{NEP}=\widehat{QPE}\)(hai góc so le trong)
Xét ΔNEP và ΔQPE có
NE=PQ(cmt)
\(\widehat{NEP}=\widehat{QPE}\)(cmt)
EP chung
Do đó: ΔNEP=ΔQPE(c-g-c)
c) Ta có: ΔNEP=ΔQPE(cmt)
nên \(\widehat{NPE}=\widehat{QEP}\)(hai góc tương ứng)
mà \(\widehat{NPE}\) và \(\widehat{QEP}\) là hai góc ở vị trí so le trong
nên EQ//NP(Dấu hiệu nhận biết hai đường thẳng song song)
hay EF//NP(đpcm)
Ta có: ΔNEP=ΔQPE(cmt)
nên NP=QE(hai cạnh tương ứng)
mà \(EF=\dfrac{1}{2}QE\)(F là trung điểm của QE)
nên \(EF=\dfrac{1}{2}\cdot NP\)(đpcm)

a, xét tam giác QIN và tam giác NKQ có L QN chung
góc MQN = góc MNQ do tam giác MNQ cân tại M (gT)
góc QIN = góc NKQ = 90
=> tam giác QIN = tam giác NKQ (ch-gn)
b, tam giác QIN = tam giác NKQ (Câu a)
=> QI = NK (đn)
QI + MI = MQ
NK + MK = MN
MN = MQ do tam giác MNQ cân tại M (gt)
=> MI = MK
=> tam giác MIK cân tại M (đn)
c, xét tam giác MIH và tam giác MKH có : MH chung
IM = MK (Câu b)
góc MIH = gics MKH = 90
=> tam giác MIH = tam giác MKH (ch-cgv)
d, tam giác MIK cân tại M (Câu b)=> góc MIK = (180 - góc IMK) : 2(tc)
tam giác MNQ cân tại M (gt) => gics MQN = (190 - góc IMK) : 2(tc)
=> góc MIK = góc MQN mà 2 góc này đồng vị
=> IK // QN (tc)
a. Vì \(\Delta MNQ\) cân tại M => \(MN=MQ,\widehat{MQN}=\widehat{MNQ}\)
Xét 2 tam giác vuông là \(\Delta NIQ\) và \(\Delta QKN\) ta có:
Cạnh chung NQ, \(\widehat{KNQ}=\widehat{IQN}\) ( vì \(\widehat{MNQ}=\widehat{MQN}\) )
\(\Rightarrow\Delta NIQ=\Delta QKN\)( cạnh huyền - góc nhọn )
b. Vì \(\Delta NIQ=\Delta QKN\Rightarrow IQ=KN\) ( 2 cạnh tương ứng )
Mà \(MN=MQ\Rightarrow MN-NK=MQ-IQ\Rightarrow MK=MI\)
\(\Rightarrow\Delta MKI\) cân tại M. ( ĐPCM )
c. Xét 2 tam giác vuông là \(\Delta MKH\) và \(\Delta MIH\) ta có:
\(MK=MI\left(cmt\right)\) và cạnh chung MH
\(\Rightarrow\Delta MKH=\Delta MIH\) ( cạnh huyền - cạnh góc vuông )
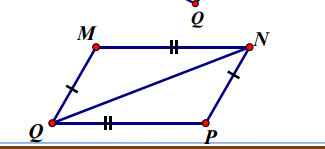
Xét \(\Delta MQN\) và \(\Delta PNQ\) có:
\(\widehat{NQP}=\widehat{MNQ}\) (Vì \(MN//PQ\) nên đó là hai góc so le trong)
\(\widehat{MQN}=\widehat{QNP}\) ( Vì \(MQ//NP\) nên hai góc đó là góc so le trong)
\(QN\) là cạnh chung
\(\Rightarrow\Delta MQN=\Delta PNQ\left(g-c-g\right)\)
a) Do △MQN=△PNQ nên
\(\Rightarrow MN=PQ\) (2 cạnh tương ứng)
b) Do △MQN=△PNQ nên
\(\Rightarrow MQ=NP\) (2 cạnh tương ứng)