Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

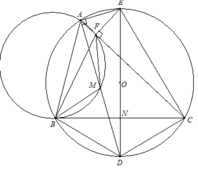
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).

Bài này là định lý khá cơ bản của tứ giác điều hoà.
Do AM, AC đẳng giác của góc BAD nên dễ dàng chứng minh được:
\(\widehat{BAM}=\widehat{CAD}\).
Mặt khác do tứ giác ABCD nội tiếp nên \(\widehat{ABM}=\widehat{ACD}\).
Từ đó \(\Delta ABM\sim\Delta ACD(g.g)\)
\(\Rightarrow\dfrac{AB}{BM}=\dfrac{AC}{CD}\Rightarrow AB.CD=BM.AC\).
Chứng minh tương tự, ta cũng có \(AD.BC=CM.AC\).
Mà BM = CM nên \(AB.CD=AD.BC\) hay tứ giác ABCD điều hoà.
(Định lý đảo vẫn đúng).

a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)
M là trung điểm AB \(\Rightarrow\overrightarrow{IM}=\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{IB}\right)\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=\left(\overrightarrow{IA}+\overrightarrow{IB}\right).\left(\overrightarrow{DI}+\overrightarrow{IC}\right)=\overrightarrow{IA}.\overrightarrow{DI}+\overrightarrow{IB}.\overrightarrow{IC}+\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}\)
\(=\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}=-IA.IC+IB.DI\)
Mặt khác do 2 tam giác vuông DIC và AIB đồng dạng (\(\widehat{IAB}=\widehat{IDC}\) cùng chắn BC)
\(\Rightarrow\dfrac{IA}{ID}=\dfrac{IB}{IC}\Rightarrow IA.IC=IB.ID\Rightarrow-IA.IC+IB.ID=0\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=0\Rightarrow IM\perp DC\)