Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
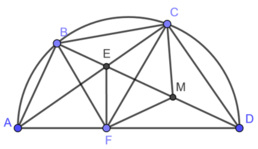
Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
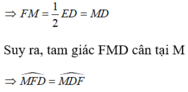
Ta có:
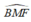là góc ngoài tại đỉnh M của tam giác FMD nên:
Xét tứ giác BCMF có:
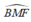và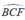 
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.
Xét $(O)$ có: $\widehat{ACD}=\widehat{ABD}=90^o$( góc nội tiếp chắn nửa đường tròn)
suy ra $\widehat{ECD}=90^o$
$\widehat{BAC}=\widehat{BDC}$ (các góc nội tiếp cùng chắn cung $BC$)
hay $\widehat{BAE}=\widehat{EDC}(1)$
Xét tứ giác $BEFA$ có: $\widehat{ABE}=\widehat{EFA}=90^o$ (do $EF AD$)
nên $\widehat{ABE}+\widehat{EFA}=180^o$
suy ra tứ giác $BEFA$ nội tiếp
suy ra $\widehat{EFB}=\widehat{BAE}(2)$ (các góc nội tiếp cùng nhắn $BE$)
Chứng minh tương tự ta có: tứ giác $ECDF$ nội tiếp nên $\widehat{EFC}=\widehat{EDC}(3)$ (các góc nội tiếp cùng chắn cung $EC$)
Từ $(1)(2)(3)$ suy ra $\widehat{EFB}+\widehat{EFC}=\widehat{BAE}+\widehat{EDC}=2.\widehat{EDC}$
hay $\widehat{BFC}=2.\widehat{EDC}$
Lại có: tam giác $ECD$ vuông tại $C$
$M$ là trung điểm $ED$
Nên $EM=MD=CM$
Suy ra tam giác $MCD$ cân tại $M$
nên $\widehat{MCD}=\widehat{MDC}$
Lại có: $\widehat{BMC}$ là góc ngoài tam giác $MCD$ nên
$\widehat{BMC}=\widehat{MCD}+\widehat{MDC}=2.\widehat{MDC}=2.\widehat{EDC}
Mà $\widehat{BFC}=2.\widehat{EDC}$
nên $\widehat{BMC}=\widehat{BFC}$
suy ra $F;M$ cùng nhìn đoạn $BC$ dưới 1 góc ko đổi
$F;M$ là 2 đỉnh liên tiếp tứ giác $BCMF$
suy ra tứ giác $BCMF$ nội tiếp (Bài toan quỹ tích cung chứa góc)
Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ
Tự vẽ hình nha ><
a) ^ABD = 900 => ^ABE = 900
EF \(\perp\)AD => ^EFA = 900
=> Tứ giác ABEF có tổng 2 góc đối = 900 nội tiếp được đường tròn
bạn tự vẽ hình nha
a)Xét tứ giác ABEF có
góc ABE=90 độ( góc nội tiếp chắn nửa dường tròn)
và góc AFE=90 độ (EF vuông góc AD tại F)
=> góc ABE + góc AFE =180 độ
=> tứ giác ABEF nội tiếp dường tròn đường kính AE
b)Ta có : góc CBD=góc CAD ( góc nội tiếp cùng chắn cung CD của (O))
và góc CAD =góc FBD (góc nội tiếp chắn cung EF của đường tròn ngoại tiếp tứ giác ABEF)
=>góc CBD=góc FBD (=góc CAD)
=>BD là tia phân giác của góc CBF
c)Xét tứ giác CEFD có:
góc DCA=90 độ (góc nội tiếp chắn nửa đường tròn)
và góc EFD=90 độ (EF vuông góc AD tại F)
=> góc DCA+góc EFD=180 độ
=> tứ giác CEFD nội tiếp dường tròn đường kính ED)
Ta có tam giác ABE vuông tại B có dường trung tuyến BM (M là trung diểm của AE)
=>BM=1/2. AE= AM=ME =>tam giác ABM cân tại M => góc ABM= góc BAM
mà góc ABM +góc MBF+góc FBE=90 độ
và góc FBE=góc CAD (cmt)
=>góc MBF+ góc CAD+ góc BAM =90 độ
mà góc ADB+ góc CAD+góc BAM =90 độ(góc BAD=góc BAM+goc1CAD)
=>góc MBF=góc ADB
mà góc ADB = góc FCM ( góc nội tiếp cùng chắn cung EF của đường tròn ngoại tiếp tứ giác CEFD)
=>góc MBF= góc FCM (=góc ADB)
=>tứ giác BMFC nội tiếp đường tròn
#B
a) Ta có: ^ABD = 90o ( góc nội tiếp chắn cung AD ( nửa đường tròn ) )
và ^AFE = 90o ( EF vuông AD)
=> ^ABD + ^AFE = 180o
=> ABEF nội tiếp
Chứng minh tương tự với DCEF
b) ABCD nội tiếp => ^ACB = ^ADB ( cùng chắn cung AB )
DCEF nội tiếp => ^ECF = ^EDF ( cùng chắn cung EF ) => ^ACF = ^ADB
=> ^ACB = ^ACF
=> CA là phân giác ^BCF
